Задача № 3

Найти производные функций:

Решение

а) Функция представляет собой частное двух функций. Ее производная по правилу дифференцирования частного равна:

$y^{\text{'}}={\left(\frac{x^2{\left(1-x\right)}^3}{1+x}\right)}^{\text{'}}=\frac{{\left(x^2{\left(1-x\right)}^3\right)}^{\text{'}}\left(1+x\right)-x^2{\left(1-x\right)}^3{\left(1+x\right)}^{\text{'}}}{{\left(1+x\right)}^2}.$

Выражение x²(1 - x)³ есть произведение двух функций: x² и (1 - x)³. Применяя правило дифференцирования произведения, имеем:

(x² · (1 - x)³)^' = (x²)^' · (1 - x)³ + x² · ((1 - x)³)^'.

Производная (1 - x²)^' = 2 · x. Функция (1 - x)³ есть сложная функция, поэтому ее производная равна:

((1 - x)³)^' = 3 · (1 - x)² · (1 - x)^' = 3 · (1 - x)² · ((1)^'-(x)^') = 3 · (1 - x)² · (0 - 1) = -3 · (1 - x)².

Производную функции (1 - x) нашли, используя формулы дифференцирования суммы двух функций. Аналогично, (1 + x)^' = 0 + 1 = 1.

Собирая все результаты, получим:

$y^{\text{'}}=2x\frac{{\left(1-x\right)}^3}{1+x}-3x^2\frac{{\left(1-x\right)}^2}{1+x}-x^2\frac{{\left(1-x\right)}^3}{{\left(1+x\right)}^2}.$

б) Последовательно дифференцируем сложную функцию, взяв за аргумент y = sin(cos²(tg³x)) и применяя последовательно правила дифференцирования сложной функции и производную синуса, косинуса и тангенса, получим:

$y^{\text{'}}=\frac{\cos \left({\cos }^2\left({\mathrm{tg}}^3\left(x\right)\right)\right)·2\cos \left({\mathrm{tg}}^3\left(x\right)\right)·\left(-\sin \left({\mathrm{tg}}^3\left(x\right)\right)\right)·3{\mathrm{tg}}^{2}x}{{\cos }^{2}x}=$

$=-6·\frac{\cos \left({\cos }^2\left({\mathrm{tg}}^{3}x\right)\right)·\cos \left({\mathrm{tg}}^{3}x\right)·\sin \left({\mathrm{tg}}^{3}x\right)·{\mathrm{tg}}^{2}x}{{\cos }^{2}x}.$

в) Наша функция есть сложная логарифмическая, в которой аргументом является выражение $u=\frac{5+3\cos x+4\sin x}{3+5\cos x}.$ Применив формулу производной логарифмической функции, получим:

$y^{\text{'}}={\left(\ln \frac{5+3\cos x+4\sin x}{3+5\cos x}\right)}^{\text{'}}=\frac{1}{\frac{5+3\cos x+4\sin x}{3+5\cos x}}{\left(\frac{5+3\cos x+4\sin x}{3+5\cos x}\right)}^{\text{'}}.$

Далее нам нужно найти производную частного двух функций. По формуле производной частного имеем:

${\left(\frac{5+3\cos x+4\sin x}{3+5\cos x}\right)}^{\text{'}}=\frac{{\left(5+3\cos x+4\sin x\right)}^{\text{'}}\left(3+5\cos x\right)-\left(5+3\cos x+4\sin x\right){\left(3+5\cos x\right)}^{\text{'}}}{{\left(3+5\cos x\right)}^2}=$

$=\frac{\left(3\sin x-4\cos x\right)\left(3+5\cos x\right)-\left(5+3\cos x+4\sin x\right)\left(-5\sin x\right)}{{\left(3+5\cos x\right)}^2}=$

$=\frac{34\sin x-12\cos x+30\sin x\cos x-20{\cos }^{2}x+20{\sin }^{2}x}{{\left(3+5\cos x\right)}^2}.$

Окончательно получим:

$y^{\text{'}}=\frac{34\sin x-12\cos x+30\sin x\cos x-20{\cos }^{2}x+20{\sin }^{2}x}{{\left(3+5\cos x\right)}^2}·\frac{1}{\frac{5+3\cos x+4\sin x}{3+5\cos x}}=$

$=\frac{34\sin x-12\cos x+30\sin x\cos x-20{\sin }^{2}x+20{\cos }^{2}x}{\left(3+5\cos x\right)\left(5+3\cos x+4\sin x\right)}.$

г) Вычисляем по формуле производной сложной функции, приняв за аргумент выражение $u=\frac{5-2x}{2\sqrt{5x-x^2}},$ получим:

$y^{\text{'}}={\left(\mathrm{arcctg}\frac{5-2x}{2\sqrt{5x-x^2}}\right)}^{\text{'}}=\frac{1}{1+{\left(\frac{5-2x}{2\sqrt{5x-x^2}}\right)}^2}{\left(\frac{5-2x}{2\sqrt{5x-x^2}}\right)}^{\text{'}}.$

Воспользовавшись формулой производной для частного двух функций и делая необходимые преобразования, получим:

$y^{\text{'}}=\frac{1}{1+{\left(\frac{5-2x}{2\sqrt{5x-x^2}}\right)}^2}·\frac{{\left(5-2x\right)}^{\text{'}}2\sqrt{5x-x^2}-\left(5-2x\right){\left(2\sqrt{5x-x^2}\right)}^{\text{'}}}{4\left(5x-x^2\right)}=$

$=\frac{1}{1+{\left(\frac{5-2x}{2\sqrt{5x-x^2}}\right)}^2}·\frac{-4\sqrt{5x-x^2}-\left(5-2x\right)\frac{5-2x}{\sqrt{5x-x^2}}}{4\left(5x-x^2\right)}=\frac{1}{\sqrt{5x-x^2}}.$

НАВЕРХ

Задача № 4

Найти неопределенные интегралы:

Решение

а) Представим подынтегральную функцию в виде алгебраической суммы двух слагаемых. Для этого разделим почленно числитель на знаменатель:

$\int \frac{{\left(1+x\right)}^2}{x^2+1}\mathrm{dx}=\int \frac{x^2+2x+1}{x^2+1}=\int 1\mathrm{dx}+\int \frac{2x}{x^2+1}\mathrm{dx}=x+\ln (x^2+1)+C.$

Неопределенный интеграл алгебраической суммы функций равен алгебраической сумме неопределенных интегралов этих функций.

б) При нахождении этого интеграла воспользуемся методом подстановки. Введем новую переменную t = 1 + 2 cosx, dt = -2 sinx dx.

Тогда:

$\int \frac{\sin x}{\sqrt[5]{1+2\cos x}}\mathrm{dx}=-\frac{1}{2}\int \frac{d(1+\cos 2x)}{\sqrt[5]{1+2\cos x}}=-\frac{1}{2}{t}^{\frac{1}{5}}\mathrm{dt}=-\frac{1}{2}\frac{5}{4}{t}^{\frac{4}{5}}+C=-\frac{5}{8}{\left(1+2\cos x\right)}^{\frac{4}{5}}+C.$

в) $\int {\mathrm{tg}}^{3}x\mathrm{dx}$ будем искать по табличной формуле $\int {\mathrm{tg}}^n\mathrm{xdx}=\frac{{\mathrm{tg}}^{n-1}x}{n-1}-\int {\mathrm{tg}}^{n-2}x\mathrm{dx}.$

Поэтому

$\int {\mathrm{tg}}^{3}x\mathrm{dx}=\frac{{\mathrm{tg}}^{2}x}{2}-\int \mathrm{tgxdx}=\frac{{\mathrm{tg}}^{2}x}{2}+\ln \cos x.$

г) Для нахождения этого интеграла воспользуемся формулой интегрирования по частям $\int f\mathrm{dg}=f·g-\int g\mathrm{df}.$ Положим f = x², dg = sin2xdx, df = 2xdx, $g=-\frac{1}{2}\cos 2x.$ Получаем:

$\int x^2\sin 2x\mathrm{dx}=-\frac{x^2}{2}\cos 2x-\int -\frac{1}{2}\cos 2x·2x\mathrm{dx}=-\frac{x^2}{2}+\int x·\cos 2x\mathrm{dx}=$

$=-\frac{x^2}{2}\cos 2x+\frac{x}{2}\sin 2x+\frac{1}{4}\cos 2x.$

НАВЕРХ

Задача № 5

Вычислить площадь фигуры, ограниченной линиями y = ax² + bx и y = cx² + dx.

Решение:

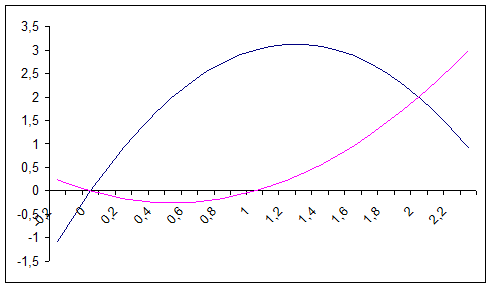
Чтобы наглядно представить фигуру, площадь которой надо найти, начертим графики функций y = x² - x и y = -2x² + 5x.

Рисунок 1

Для построения параболы y = x² - x определим координаты ее вершины и точек пересечения с осями координат. Разложив уравнение y = x² - x = (x - 1) · x, получим координаты вершины параболы A(0,5; -0,25). Ветви параболы направлены вверх, так как коэффициент при x², равный 1, положителен. Точки пересечения параболы с осью абсцисс найдем, решив квадратное уравнение x² - x = 0. Корни этого уравнения x₁ = 0; x₂ = 1. Получили точки O(0; 0); A₁(1; 0). Точка пересечения с осью ординат находится при x = 0. Эта точка совпадает с точкой A. Для построения второй параболы y = -2x² + 5x необходимо провести аналогичные действия. Получим вершину B(1,25; 3,125) и точки O(0; 0); B₁ (2,5; 0). Ветви этой параболы направлены вниз, так как коэффициент при x² отрицателен. На рисунке 1 построены обе параболы. Ограниченная параболами часть плоскости является фигурой, площадь которой надо найти. Для определения абсцисс точек пересечения парабол решим уравнение x² - x = -2x² + 5x или 3x² - 6x = 0, откуда x₁ = 0; x₂ = 2.

Площадь фигуры вычисляем по формуле

$S=\underset{a}{\overset{b}{\int }}[f\left(x\right)-g\left(x\right)]\mathrm{dx}$

где f(x) ≥ g(x) для всех x ∈ [a; b].

В нашем случае a = x₁ = 0; b = x₂ = 2. На отрезке [0; 1] имеем -2x² + 5x ≥ x² - x. Поэтому

f(x) = -2x² + 5x и g(x) = x² - x.

Следовательно,

$S=\underset{0}{\overset{2}{\int }}[\left(-2x^2+5x\right)-(x^2-x)]\mathrm{dx}=\underset{0}{\overset{2}{\int }}\left(-3x^2+6x\right)\mathrm{dx}.$

Для вычисления определенного интеграла применяется формула Ньютона-Лейбница:

$\underset{a}{\overset{b}{\int }}f\left(x\right)\mathrm{dx}=F\left(x\right){\mid }_a^b=F\left(b\right)-F\left(a\right),$

где F(x) - первообразная подынтегральной функции f(x).

Окончательно

$S=\underset{0}{\overset{2}{\int }}\left(-3x^2+6x\right)\mathrm{dx}=(-x^3+3x^2){\mid }_0^2=-2^3+3·2^2-0=4.$

Программа MalMath - пошаговый решатель представляет собой полноценный инженерный калькулятор. Предназначена для работы на устройствах, управляемых операционной системой Android. Помимо традиционных арифметических, алгебраических  и тригонометрических вычислений, MalMath решает уравнения, вычисляет пределы функций, находит производные, вычисляет интегралы и осуществляет массу других математических операций.

MalMath можно назвать аналогом MathCAD для Android. Знакомые с работой в MathCAD легко и непринужденно освоят MalMath. В программу заложена масса полезных свойств, облегчающих работу пользователя. Программа распознает ошибки во вводимых данных, выдаст понятные предупреждения о них.

В процессе решения задач MalMath подробно описывает каждый свой шаг. Программа укажет ресурсы сети, объясняющие методы конкретных решений, четко обоснует необходимость применения метода, гиперссылки приведут к справочной литературе.

---

Пользуйся браузерами Yandex, Firefox, Opera, Edge - они правильно отражают формулы, встречающиеся на страницах, как в десктопном, так и в мобильном вариантах.

Отключи на минуту блокираторы рекламы и нажми на пару баннеров на странице. Тебе ничего не будет стоить, а сайту поможешь материально.

---