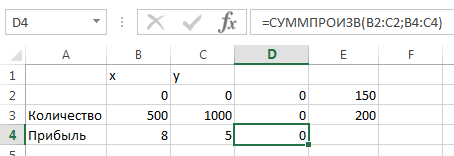
Рис. 1. Форма для решения задачи - числовые значения
Фирма выпускает ковбойские шляпы двух фасонов (А и В). Трудоемкость изготовления шляпы фасона А вдвое выше трудоемкости изготовления шляпы фасона В. Если бы фирма выпускала только шляпы фасона А, суточный объем производства мог бы составить 500 шляп. Суточный объем сбыта шляп обоих фасонов ограничен диапазоном от 150 до 200 штук. Прибыль от продажи шляпы фасона А равна $8, а фасона В - $5. Определить, какое количество шляп каждого фасона следует изготовить, чтобы максимизировать прибыль.
Если бы фирма выпускала только шляпы фасона В, суточный объем производства мог бы составить 500 ∙ 2 = 1000 шляп. Пусть фирма выпускает в сутки x шляп фасона А и y шляп фасона В.
Создадим математическую модель задачи сформулировав целевую функцию и ограничения.
8 ∙ x + 5 ∙ y → max;
Построим на рабочем листе Excel форму для решения задачи.

Рис. 1. Форма для решения задачи - числовые значения
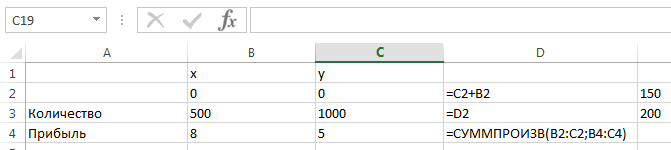
Рис. 2. Форма для решения задачи - формульный вид
Ячейка D4 содержит формулу целевой функции
=СУММПРОИЗВ(B2:C2;B4:C4).
Применим инструмент Excel «Поиск решения» для решения задачи.
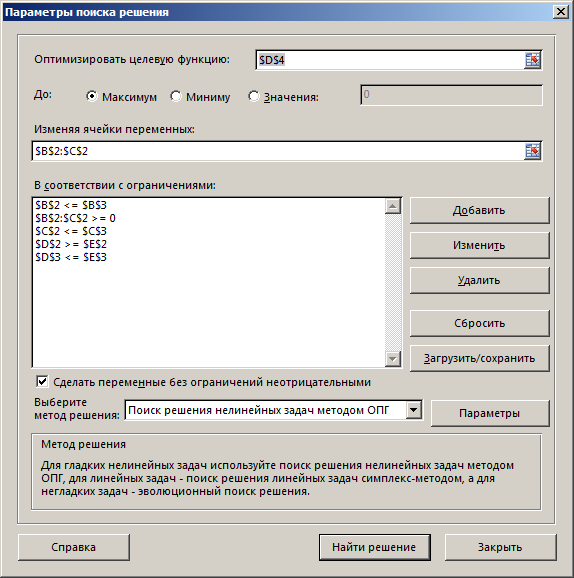
Рис. 3. Настройки инструмента «Поиск решения»
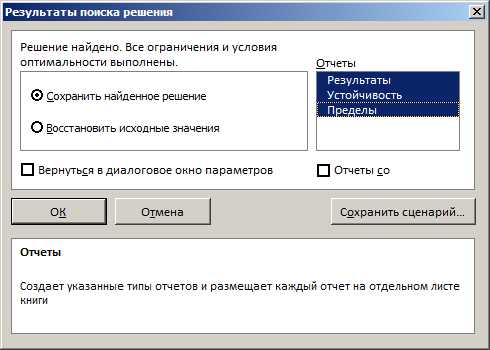
Рис. 4. Отчет о результатах применения инструмента «Поиск
решения»
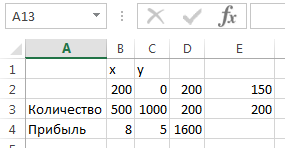
Рис. 5.
Результат применения инструмента «Поиск решения»
Вывод: Для получения максимальной прибыли при ограничениях, представленных в условии, необходимо произвести 200 шляп фасона А, шляпы фасона В производить не надо. При этом прибыль составит 1600$.
Отчеты Excel по решению данной задачи:
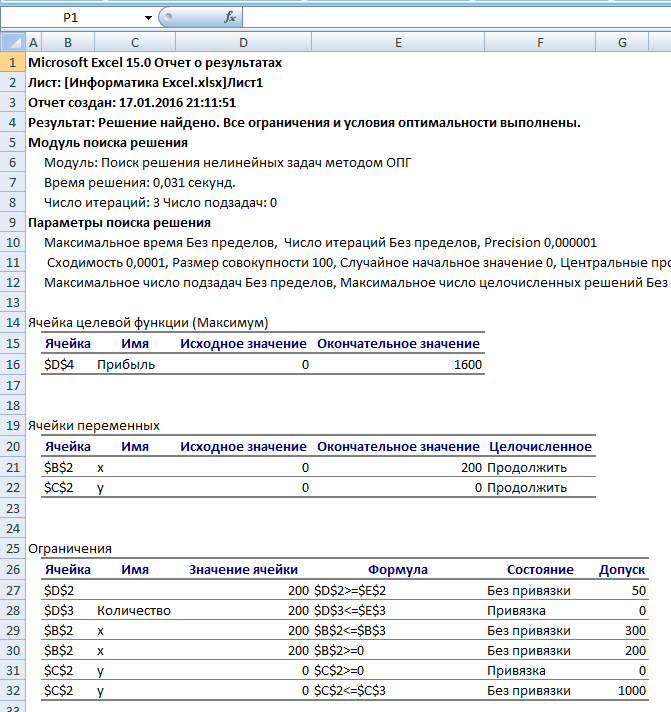
Рис. 6. Отчет о
результатах
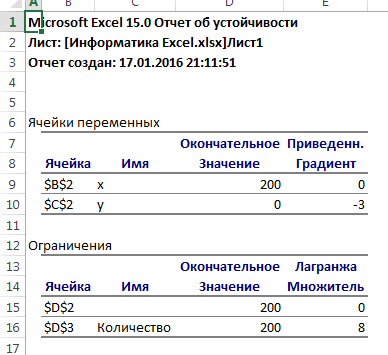
Рис. 7. Отчет об
устойчивости
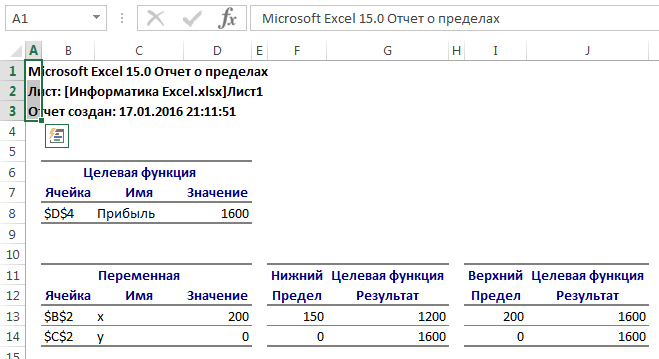
Рис. 8. Отчет о
пределах