Глава 1. Образовательная система России
Глава 2. Автоматизация учебного процесса
Глава 3. Основы теории тестирования
Глава 4. Базы заданий для проектирования тестов
Глава 5. Модели и алгоритмы проектирования тестов
Глава 6. Автоматизация проектирования тест-билетов
Глава 7. Методические и технологические аспекты тестирования
Глава 4. Базы заданий для проектирования тестов.
4.1. Параметры тестовых заданий.
Для описания баз тестовых заданий и проектирования тест-билетов удобно подразделять параметры заданий на три категории: технологические, экспертные и статистические.
К технологическим относят параметры, описывающие задания с технической (не содержательной) точки зрения. Как правило, эти характеристики допускают однозначное толкование. Примеры таких параметров:
- тип заданий:
- закрытое - задание, форма представления которого допускает дихотомическую оценку правильности -верно / неверно. Проверка таких заданий не требует привлечения педагогов;
- открытое - задание, форма представления которого требует для проверки привлечения педагогов: задания открытого типа обычно проверяются по многобалльной шкале (чаще всего (10+1) - балльной):
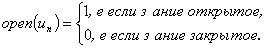
- форма представления информации:
- текст ui ∈ Gtext,
- графика ui ∈ Gpicter,
- фото ui ∈ Gfoto,
- аудио ui ∈ Gaudio,
- видео ui ∈ Gvideo,
- время представления задания (для аудио- и видеотестовых заданий) τn
- возможность компьютерного представления ui ∈ Gcomp.
- место (в мм), необходимое для выполнения задания,
- требуемый объем памяти компьютера (внешние накопители) для хранения заданий (файла заданий),
- количество заданий в файле.
К экспертным относят параметры, значения которых описываются экспертами. Примеры таких параметров:
- количество учебных элементов pi,
- время выполнения задания tn,
- сложность (уровень усвоения знаний) αi,
- ступень абстракции βi,
- степень осознанности усвоения знаний βi ,
- экспертная трудность.
К статистическим относят параметры тестовых заданий, которые вычисляются по результатам пилотных испытаний (предтестирование). По мере проведения педагогических измерений статистика может накапливаться и могут вноситься соответствующие коррективы. Примеры статистических параметров:
1) коэффициент решаемости задания ki
2) коэффициенты селективности задания Di и ripb ,
3) коэффициент привлекательности дистракторов,
4) параметры логистических кривых:
- дифференцирующая способность задания ai ,
- трудность задания bi,
- коэффициент угадывания ci.
4.2. Структура базы заданий.
При разработке структуры базы заданий возникает вопрос о том, какие параметры заданий должны быть описаны. Ответ на этот вопрос зависит от тех моделей, которыми пользуется составитель при проектировании тест-билета.
Так для проектирования тест-билетов с помощью процедуры В.П. Беспалько [13, 36] структура базы заданий должна иметь следующий вид:
| Наименование задания | Перечень учебных элементов | Параметры | ||
|---|---|---|---|---|
| α | β | γ | ||
Если используются классические процедуры, то в качестве основных (статистических) параметров должны быть указаны коэффициент решаемости и коэффициент селективности.
В этом случае базы заданий должны иметь следующую структуру:
| Наименование задания | Коэффициент решаемости ki | Коэффициент селективности Di | Коэффициент решаемости дистракторов | |||
|---|---|---|---|---|---|---|
| ki(1) | ki(2) | ki(3) | ki(4) | |||
Классические параметры существенно (и часто нелинейно) зависят от популяции тестируемых, на которых была получена статистика. При разработке тест-билетов классические параметры (они интуитивно более понятны удобны на этапе первичного конструирования тест-билета либо когда база заданий используется примерно для той же категории испытуемых, на которых проводилась калибровка заданий, при стабильном учебном процессе в школе, вузе и т. д.
Параметры логистических кривых являются инвариантными (точнее - зависят линейно) при переходе от одной группы тестируемых к другой. Это свойство делает их весьма практичными при проектировании тест-билетов для любой популяции тестируемых и позволяет использовать широкий спектр процедур проектирования тест-билетов.
4.3. Калибровка заданий. Экспертные методы.
Процедуру описания характеристик заданий называют калибровкой. Одним из наиболее простых экспертных методов калибровки является метод комиссии.
Суть этого метода состоит в открытой дискуссии с целью выработки единого мнения. Каждый из членов комиссии опытных педагогов (экспертов) аргументировано обосновывает свою точку зрения по характеристикам представленных тестовых заданий. Решения о присвоении той или иной характеристики тестовому заданию достигается либо путем консенсуса, либо путем голосования.
Достоинством метода является открытое аргументированное обсуждение, когда растет уровень информированности экспертов и происходит изменение первоначальной точки зрения экспертов. Недостаток метода - возможность "давления" со стороны более авторитетных экспертов, что, однако, не гарантирует компетентности в оценке характеристик. Более того, активность ряда экспертов может не коррелировать с их компетентностью.
Другим широко распространенным методом в проведении экспертизы является метод Делфи.
Суть метода состоит в создании условий, обеспечивающих наиболее продуктивную работу экспертов.
Оценивание происходит в несколько этапов. На первом этапе аналитические группы готовят анкеты эксперта необходимую сопроводительную информацию. Анкета передается или рассылается экспертам. Для этой цели удобно использовать возможности Интернета (или электронной почты) и электронные шаблонные формы (например, формате Excel), которые позволят оперативно производит обработку полученных результатов. Обработка состоит в следующем:
- определение экспертов, предоставивших «крайние» оценки характеристик;
- усредненное мнение экспертов;
- представление разброса экспертных оценок.
На втором этапе экспертам представляются усредненные оценки экспертов и (анонимное) обоснование экспертов, предоставивших «крайние» оценки. После получения этой дополнительной информации эксперты высылаю свои новые откорректированные оценки. После обработок вновь полученной информации проводится третий этап аналогичный второму. Процедура завершается, когда оценки экспертов стабилизируются. В некоторых случая процедура охватывает четыре-пять этапов.
Как показывает опыт, метод Делфи является достаточно надежным инструментом для получения оценок экспертных характеристик тестовых заданий.
4.4. Калибровка заданий. Статистические методы
Пусть по результатам тестирования получена матриц ответов D размером NхL, причем произведена выбраковка строк и столбцов, целиком состоящих из нулей и едини! (m - для политомических заданий).
Нахождение статистических классических параметров не вызывает трудностей и проводится по формулам:
- коэффициент решаемости задания
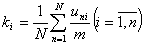
- коэффициент селективности задания
Di=k’i-k”i,
где k’i - коэффициент решаемости i-го задания лучшей половины тестируемых;
k”i - коэффициент решаемости i-го задания худшей половины тестируемых.
Вычисление статистических параметров IRT представляет более сложную задачу. Рассмотрим несколько методов ее решения.
4.4.1. Метод PROX для модели Раша.
Предложен L. Cohen в 1976 г. [36] для модели Раша. Предполагается, что тест составлен из дихотомических задний, латентные переменные испытуемых и трудность заданий в тест-билете распределены нормально:
θn≈N(M,σ2), δl≈N(H, ω2).
Алгоритм вычисления:
- Вычисляются коэффициенты решаемости заданий коэффициенты выполнения испытуемыми тест-билета:
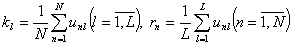 .
.
- Вычисляются (в логитах) трудность заданий и латентные переменные испытуемых:
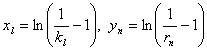 .
.
- Вычисляются средние значения и дисперсии:
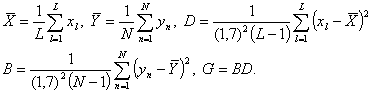
- Вычисляются поправочные коэффициенты:
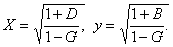
- Оценка трудности заданий βi и латентных переменных θn:
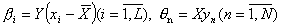 .
.
- Находятся стандартные ошибки:
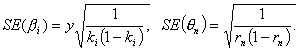
4.4.2. Метод наибольшего правдоподобия.
Рассмотрим метод наибольшего правдоподобия, который достаточно эффективен для заданий закрытого типа
Пусть вектор ui={ui1, ui2, ..., uin} - результат выполнения i-м испытуемым n закрытых заданий тест-билет где uij= 1, если задание выполнено верно, и uij=0, если задание выполнено неверно. Тогда функция правдоподобия имеет вид:
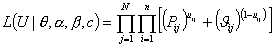 ,
,
где Pij - вероятность правильного
выполнения i-м испытуемым j-го задания тест-билета и
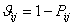 .
.
Так как функции L и ln L достигают максимума при одном и том же значении аргумента, то для вычислительных целей удобно рассматривать логарифм от функции L:
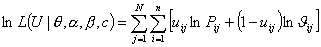 .
.
Одно из основных предположений IRT - все задания тест-билета являются локально независимыми. Предположение о локальной независимости является существенным. Оно означает, что при данном уровне знаний ответ на каждое задание тест-билета не зависит от результатов выполнения остальных его заданий.
Значения 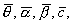 при котором
функция правдоподобия достигает максимума, принимают в качестве объективных
оценок θ, α, β, c и называют оценками наибольшего правдоподобия.
при котором
функция правдоподобия достигает максимума, принимают в качестве объективных
оценок θ, α, β, c и называют оценками наибольшего правдоподобия.
Неизвестные оценки наибольшего правдоподобия для параметров испытуемых находятся из необходимого условия экстремума функции ln Li, по каждой из переменных θ, →a, →β, c. Система уравнений для определения величины θi в группе из N испытуемых имеет вид:
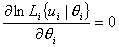 , где i=1, 2,
..., N.
, где i=1, 2,
..., N.
Уравнения системы являются нелинейными, и их решение сопряжено с определенными вычислительными трудностями. Но каждое j-е уравнение зависит только от переменной θi, следовательно, значения θi можно определять независимо.
Система уравнений для определения характеристик тест-билета из n заданий в группе имеет вид:
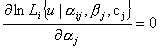 , где i=1, 2, ...,
n,
, где i=1, 2, ...,
n,
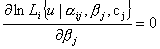
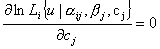
Решение систем правдоподобия проводится по очереди. Сначала полагают известными значения параметра αi, βi, ci, а θi рассматривают как переменную. Затем значения θj переопределяют, принимая за новые θj , и находят оценки αi, βi, cj доставляющие максимум функции ln Lj. На втором этапе переопределяют значения α, β, c. Процесс продолжается до тех пор, пока абсолютные значения разностей в результате итераций не станут меньше 0,01:
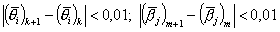 .
.
Конечно, для реализации этого метода нужны специальные программы.
Важным предварительным моментом; является выбор хорошего начального приближения
при оценивании θi и αj, βj,
cj, i=1, 2, ..., N;
j=1, 2, ..., n. Начальная оценка уровня i-го испытуемого находится
по формуле: 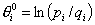 i= 1, 2, ...,
N, где N - число испытуемых, pj - доля правильных ответов
i-го испытуемого на все задания теста, qi,
- доля неправильных, т. е. qi=1-pi.
Аналогичная начальная оценка параметров j-гo задания находится по
формуле
i= 1, 2, ...,
N, где N - число испытуемых, pj - доля правильных ответов
i-го испытуемого на все задания теста, qi,
- доля неправильных, т. е. qi=1-pi.
Аналогичная начальная оценка параметров j-гo задания находится по
формуле 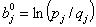 j = 1, 2, ..., n,
где n - число заданий, рj - доля правильных
ответов всех испытуемых на j-e задания теста, qi
- доля неправильных, т. е. qi=1-pj.
j = 1, 2, ..., n,
где n - число заданий, рj - доля правильных
ответов всех испытуемых на j-e задания теста, qi
- доля неправильных, т. е. qi=1-pj.
Для нахождения максимального значения функции ln L можно использовать любой метод безусловной оптимизации функций нескольких переменных. Анализ показывает, что численные методы нулевого порядка дают плохую и очень медленную сходимость (например, метод покоординатного спуска). Метод Ньютона, использующий матрицу Гессе, также дает неудовлетворительный результат из-за плохой обусловленности матрицы Гессе. Практические расчеты показали, что квазиньютоновский метод Бройдена дает хорошую и устойчивую сходимость.
4.4.3. Метод наименьших квадратов.
Для заданий открытого типа достаточно эффективным является метод наименьших квадратов. Алгоритм вычисления параметров j-го задания:
- В случае заданий открытого типа баллы за задание приводятся к диапазону [0, 1].
- Вычисляются коэффициенты выполнения испытуемыми тест-билета:
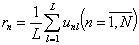
- Множество всех испытуемых делится на 11 подмножеств G0...G10 таким образом, что n-й испытуемый относится к i-й группе, если 0,1i≤ ri ≤ 0,1(i+1).
- Находятся коэффициенты решаемости l-го задания для группы Gi:
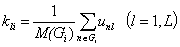 ,
,
где M(Gi)- мощность множества Gi.
Таким образом, для каждого задания l получаем таблично заданную функцию Kl(i).
- Считаем, что значение функции Kl(i) находится по формуле:
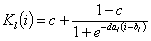
Исходя из этого, подбираем коэффициенты al, bl, cl минимизируя функцию
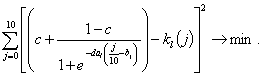
Минимизацию можно производить любым численным методом, например, методом покоординатного спуска.
4.5. Выравнивание заданий в файле.
Одна из основных и трудоемких задач при формировании банка файлов тестовых заданий - соблюдение принципа однородности, который предполагает группирование в одном файле заданий, близких по своим технологическим экспертным и статистическим характеристикам. Важным инструментом для этой цели является введение мер близости, которые позволяют определить, насколько "близки" или "далеки" друг от друга тестовые задания.
В качестве примера рассмотрим векторную меру близости v=(vk, vi, ve),
где vk - составляющая классических статистических характеристик,
vl - составляющая латентных (IRT) статистических характеристик,
ve - составляющая экспертных характеристик.
Пусть ui = (ki, Di, ai, bi, pi, αi, βi, ti) - тестовое задание с описывающими его статистическими и экспертными характеристиками (параметрами):
ki - коэффициент решаемости,
Di - коэффициент селективности (D - индекс),
аi - дифференцирующая способность,
bi - трудность,
pi - количество учебных элементов в задании,
αi - уровень усвоения,
βi - ступень абстракции,
ti - время выполнения.
Тогда ui можно идентифицировать с точкой в векторном пространстве
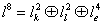 ,
,
где lk2 подпространство классических статистических параметров,
ll2 - подпространство латентных статистических параметров,
le2 - подпространство экспертных параметров.
Для каждой пары тестовых заданий ui и uj в подпространствах lk2, ll2, le2 введем обычные lq-нормы с весами:
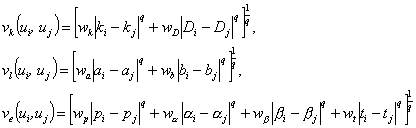
где wk ≥ 0 , wD ≥ 0 , wa ≥ 0 , wb ≥ 0 , wp ≥ 0, wα ≥ 0, wβ ≥ 0, wt ≥ 0 - весовые коэффициенты.
Тогда 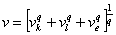 является интегрально
нормой параметров в l8.
является интегрально
нормой параметров в l8.
Одна из целей предтестирования - получение статистической информации для принятия решений о приемлемости, неприемлемости и "подозрительных" заданий могут обладать определенными техническими недостатка ми). "Подозрительные" задания не обязательно должны исключаться из банка заданий. Они лишь должны быть подвергнуты дополнительному, более тщательному анализу.
Анализ несоответствия параметров конкретного задания, содержащего его файла заданий общим параметра удобно проводить "сверху вниз", применяя карты Шухарта [36].