[an error occurred while processing this directive]

В начало

Тема 1. Введение. Эконометрика и эконометрическое моделирование

Тема 2. Временные ряды

Тема 3. Парная регрессия и корреляция

Тема 4. Модель множественной регрессии

Тема 5. Системы линейных одновременных уравнений

Тема 6. Многомерный статистический анализ

Задания для выполнения контрольной работы по дисциплине

Задания для выполнения аудиторной работы

Приложения

Литература

Полезные ссылки на Интернет-ресурсы

Задания для выполнения контрольной работы по дисциплине

Задача 1

По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений (X, млн. руб.).

Требуется:

  1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
  2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков 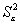; построить график остатков.
  3. Проверить выполнение предпосылок МНК.
  4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента (α = 0,05).
  5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью F-критерия Фишера (α = 0,05), найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
  6. Осуществить прогнозирование среднего значения показателя Y при уровне значимости α = 0,1, если прогнозное значение фактора X составит 80% от его максимального значения.
  7. Представить графически: фактические и модельные значения Y, точки прогноза.
  8. Составить уравнения нелинейной регрессии:
  • гиперболической;
  • степенной;
  • показательной.

Привести графики построенных уравнений регрессии.

  1. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.

Вариант 1

X 66 58 73 82 81 84 55 67 81 59
Y 133 107 145 162 163 170 104 132 159 116

Вариант 2

X 72 52 73 74 76 79 54 68 73 64
Y 121 84 119 117 129 128 102 111 112 98

Вариант 3

X 38 28 27 37 46 27 41 39 28 44
Y 69 52 46 63 73 48 67 62 47 67

Вариант 4

X 36 28 43 52 51 54 25 37 51 29
Y 104 77 117 137 143 144 82 101 132 77

Вариант 5

X 31 23 38 47 46 49 20 32 46 24
Y 38 26 40 45 51 49 34 35 42 24

Вариант 6

X 33 17 23 17 36 25 39 20 13 12
Y 43 27 32 29 45 35 47 32 22 24

Вариант 7

X 36 28 43 52 51 54 25 37 51 29
Y 85 60 99 117 118 125 56 86 115 68

Вариант 8

X 17 22 10 7 12 21 14 7 20 3
Y 26 27 22 19 21 26 20 15 30 13

Вариант 9

X 12 4 18 27 26 29 1 13 26 5
Y 21 10 26 33 34 37 9 21 32 14

Вариант 10

X 26 18 33 42 41 44 15 27 41 19
Y 43 28 51 62 63 67 26 43 61 33

Задача 2

Задача 2а и 2б

Для каждого варианта даны по две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.

Номер варианта Номер уравнения Задача 2а Задача 2б
переменные переменные
y1 y2 y3 x1 x2 x3 x4 y1 y2 y3 x1 x2 x3 x4
1 1 -1 b12 b13 0 0 a13 a14 -1 b12 b13 0 a12 a13 0
2 0 -1 b23 a21 a22 a23 0 0 -1 b23 a21 a22 0 a24
3 0 b32 -1 a31 0 a33 a34 b31 b32 -1 0 a32 a33 0
2 1 -1 0 b13 a11 a12 a13 0 -1 b12 0 a11 a12 a13 0
2 b21 -1 b23

0

0

a23 a24 0 -1 b23 a21 0 a23 a24
3 0 b32 -1 a31 0 a33 a34 0 b32 -1 a31 0 a33 a34
3 1 -1 0 b13 a11 a12 0 a14 -1 b12 b13 a11 0 0 a14
2 b21 -1 0 a21 a22

0

a24 b21 -1 0 0 a22 a23 a24
3 b31 b32 -1 0 0 a33 a34 b31 b32 -1 a31 0 0 a34
4 1 -1 b12 b13 0 a12 0 a14 -1 0 b13 a11 a12 a13 0
2 b21 -1 0 a21

0

a23 a24 0 -1 b23 a21 a22 0 a24
3 b31 b32 -1 a31 a32 0 0 b31 0 -1 a31 a32 a33 0
5 1 -1 0 b13 a11 0 a13 a14 -1 0 b13 a11 a12 a13 0
2 b21 -1 b23

0

a22

0

a24 b21 -1 b23 0 0 a23 a24
3 b31 0 -1 0 a32 a33 a34 b31 0 -1 a31 a32 a33 0
6 1 -1 b12 b13 a11 a12 0 0 -1 0 b13 a11 a12 0 a14
2 b21 -1 b23 a21

0

0

a24 b21 -1 0 a21 0 a23 a24
3 0 b32 -1 a31 a32 a33 0 b31 0 -1 a31 a32 0 a34
7 1 -1 0 b13 0 a12 a13 a14 -1 b12 b13 0 a12 0 a14
2 b21 -1 b23

0

a22 a23 0 b21 -1 0 a21 0 a23 a24
3 0 b32 -1 a31 a32 a33 0 b31 b32 -1 0 a32 0 a34
8 1 -1 b12 b13 0 a12 a13 0 -1 0 b13 a11 0 a13 a14
2 0 -1 b23 a21 a22

0

a24 b21 -1 b23 0 a22 0 a24
3 0 b32 -1 a31 a32 a33 0 b31 0 -1 a31 0 a33 a34
9 1 -1 b12 0 a11 a12 a13 0 -1 b12 b13 a11 a12 0 0
2 0 -1 b23 a21

0

a23 a24 b21 -1 b23 0 0 a23 a24
3 0 b32 -1 a31 a32 a33 0 b31 b32 -1 0 0 a33 a34
10 1 -1 b12 b13 a11 0 0 a14 -1 0 b13 0 a12 a13 a14
1 b21 -1 0

0

a22 a23 a24 b21 -1 b23 a21 0 a23 0
3 0 b32 -1 0 a32 a33 a34 b31 0 -1 0 a32 a33 a34

Задача 2в

По данным таблицы для своего варианта, используя косвенный метод наименьших квадратов, построить структурную форму модели вида:

y1 = a01 + b12y2 + a11x1 + ε1,

y2 = a02 + b21y1 + a22x2 + ε2.

Вариант n y1 y2 x1 x2 Вариант n y1 y2 x1 x2
1 1 76,7 35,4 5 7 6 1 77,5 70,7 1 12
2 94,1 37,9 7 7 2 100,6 94,9 2 16
3 88,2 40,8 6 9 3 143,5 151,8 7 20
4 126,9 47,3 10 10 4 97,1 120,9 8 10
5 111,0 61,5 7 18 5 63,6 83,4 6 5
6 50,1 26,6 3 4 6 75,3 84,5 4 9
2 1 28,3 51,7 7 12 7 1 61,3 31,3 9 7
2 4,4 11,5 1 1 2 88,2 52,2 9 20
3 33,1 64,6 10 14 3 38,0 14,1 4 2
4 14,6 38,4 9 4 4 48,4 21,7 2 9
5 35,9 64,1 7 17 5 57,0 27,6 7 7
6 39,5 55,0 1 20 6 59,7 30,3 3 13
3 1 29,9 75,3 2 8 8 1 51,3 39,4 3 10
2 89,8 114,3 8 3 2 112,4 77,9 10 13
3 36,3 66,2 3 3 3 67,5 45,2 5 3
4 83,5 160,2 6 19 4 51,4 37,7 3 7
5 112,9 180,5 9 17 5 99,3 66,1 9 6
6 74,5 97,1 7 1 6 57,1 39,6 4 1
4 1 31,3 60,2 4 8 9 1 25,1 21,8 8 7
2 35,1 74,2 7 5 2 41,7 33,8 10 14
3 31,2 59,7 4 8 3 12,5 12,5 7 1
4 40,4 107,0 9 13 4 25,9 23,4 7 8
5 25,3 29,2 1 4 5 41,7 36,0 5 17
6 41,2 112,5 10 12 6 9,4 11,4 2 2
5 1 73,9 75,0 5 11 10 1 98,9 68,2 6 8
2 88,6 67,3 8 7 2 57,9 46,0 1 7
3 34,3 34,9 2 3 3 96,3 69,6 5 9
4 84,5 86,3 6 13 4 140,5 104,7 4 20
5 42,7 64,5 1 11 5 118,5 82,1 6 12
6 103,5 93,4 8 14 6 63,9 48,8 3 5
[an error occurred while processing this directive]