Тема 1. Оптимизационные экономико-математические модели
Тема 2. Методы получения оптимальных решений
Тема 4. Методы и модели анализа экономических процессов
Тема 5. Прогнозирование экономических процессов с использованием временных рядов
Тема 6. Производственные функции
Тема 7. Методы и модели управления и принятия решений в экономических системах
Тема 1. Оптимизационные экономико-математические модели
1.1. Экономические основы оптимизации. Принцип оптимальности в планировании и управлении. Общая запись оптимизационной экономической задачи (ЭММ оптимизации). Классическая задача оптимизации, метод реализации. Общая классификация оптимизационных моделей и методов их реализации.
1.2. Примеры экономико-математических моделей оптимизации.
1.3. Технология компьютерной реализации оптимизационных моделей стандартными офисными средствами (в среде пакета Excel).
Оптимизационные (экстремальные) модели в экономике возникают при практической реализации принципа оптимальности в управлении.
Необходимым условием использования принципа оптимальности (оптимального подхода к планированию и управлению) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать те или иные управленческие решения. Именно такими, как правило, и являются ситуации, составляющие повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей и загрузка контейнеров и т.д.).
Суть принципа оптимальности состоит в стремлении выбрать такое управленческое решение Х = (х1, х2, …, хn), где хj, j = 1, ..., n, - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
«Наилучшим образом» здесь означает выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных управленческих решений. Традиционные критерии оптимальности в экстремальных моделях — «максимум прибыли», «минимум затрат», «максимум объема работ (услуг)» и др.
«Учитывало бы внутренние возможности и внешние условия производственной деятельности» означает, что на выбор управленческого решения (поведения) накладывается ряд условий, т.е. выбор X осуществляется из некоторой области возможных (допустимых) решений D.
Таким образом, реализовать на практике принцип оптимальности в планировании и управлении — это значит решить экстремальную задачу вида:
max (min) f(X) (1.1)
X ∈ D (1.2)
где f(X) - математическая запись критерия оптимальности - целевая функция.
Задачу условной оптимизации (1.1), (1.2) обычно записывают в виде:
найти максимум или минимум функции
f(X) = f(х1, х2, … хn) (1.3)
при ограничениях
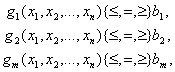 (1.4)
(1.4)
xj ≥ 0, j = 1, 2, ..., n. (1.5)
Условие (1.5) необязательно, но его всегда можно добиться. Обозначение {≤, =, ≥} говорит о том, что в конкретном ограничении возможен один из знаков <, = или >. Более компактная запись выглядит следующим образом:
max (min) f(х1, х2, … хn) (1.6)
gi(x1, x2, …, хn) {≤, =, ≥} bi, i = 1, 2, ..., m (1.7)
xj ≥ 0, j = 1, 2, ..., n. (1.8)
Задача (1.6)—(1.8) — общая задача оптимального (математического) программирования, другими словами, математическая модель задачи оптимального программирования в основе построения (разработки) которой лежат принципы оптимальности, системности и адекватности.
Областью определения или областью допустимых решений задачи оптимального программирования принято называть всю совокупность (множество) ее допустимых решений.
Вектор X (набор управляющих переменных хj, j = 1, 2, ..., n) называется допустимым решением или планом задачи оптимального программирования, если он удовлетворяет системе ограничений (1.7)-(1.8). А тот план X (допустимое решение), который доставляет максимум или минимум целевой функции f(х1, х2, …, хn) называется оптимальным планом (оптимальным поведением или просто решением) задачи оптимального программирования.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности, адекватности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (задача противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи и (или) разработанной ЭММ. Например, имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно и некоторые существенные ограничения в ней отсутствуют.
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными —
а) линейные,
б) нелинейные.
В случае а) все функциональные связи в системе ограничений и функция цели — линейные функции; наличие нелинейности в хотя бы одном из упомянутых элементов приводит к случаю б).
2. По характеру изменения переменных —
а) непрерывные,
б) дискретные.
В случае а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область, в случае б) все или хотя бы одна переменная могут принимать некоторые целочисленные значения.
3. По учету фактора времени —
а) статические,
б) динамические.
В задачах а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается управленческое решение; в случае б) такое предположение достаточно аргументировано принято не может быть.
4. По наличию информации о переменных —
а) задачи в условиях полной определенности (детерминированные),
б) задачи в условиях неполной информации (случай риска),
в) задачи в условиях неопределенности.
В задачах б) отдельные элементы являются вероятностными величинами, однако дополнительными статистическими исследованиями могут быть установлены их законы распределения вероятностей; в случае в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.
5. По числу критериев оценки альтернатив —
а) простые (однокритериальные),
б) сложные (многокритериальные) задачи.
Задачи а) — задачи, где экономически приемлемо использование одного критерия оптимальности или удается специальными процедурами (например «взвешиванием приоритетов») свести многокритериальный поиск к однокритериальному; б) многокритериальная оптимизация — выбор управленческого решения по нескольким показателям.
На практике многокритериальный поиск тем или иным способом сводят к однокритериальному: методом последовательных уступок, способом выделения «главного» показателя, оптимизацией по обобщенной целевой функции и др.
Например, при оптимизации по обобщенной целевой функции она может быть записана следующим образом:
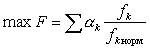 (суммирование k =
1, 2, ..., s),
(суммирование k =
1, 2, ..., s),
где fk - k-я целевая функция;
fk норм - нормирующее значение k-й целевой функции;
αk — коэффициент веса k-й целевой функции;
s — число критериев (целевых функций).
При этом перед составляющими целевой функции, которые максимизируются, ставится знак плюс, перед минимизируемыми - минус. Значения fk норм принимаются при максимизации k-й составляющей целевой функции: fk норм = fk max при ее минимизации — fk норм = fk min.
Коэффициенты веса каждого оптимизируемого показателя могут быть определены методом экспертных оценок, например процедурой непосредственного назначения экспертами коэффициентов веса. В этом случае каждый эксперт оценивает сравнительную важность рассматриваемых показателей, которые будут входить в целевую функцию. Для каждого j-го показателя i-й эксперт должен назначить коэффициент веса aij, так чтобы сумма всех коэффициентов веса, назначенных одним экспертом для различных показателей, равнялась единице:
Σaij = 1, i = 1, 2, ..., n,
где n — число экспертов.
В качестве коэффициента веса k-й целевой функции ak можно взять среднее значение aik по всем экспертам.
С учетом сказанного в дальнейшем будем рассматривать однокритериальные задачи оптимизации.
Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например:
- 1а2а3а4а5а — задачи и методы линейного программирования;
- 1б2а3а4а5а - задачи и методы нелинейного программирования;
- 1а2б3а4а5а - задачи и методы целочисленного программирования и т.д.
Рассмотрим пример постановки и разработки оптимизационной ЭММ.
Постановка задачи. На некоторый временной период, например месяц, осуществляется формирование производственной программы выпуска двух видов изделий Р1 и Р2. Для их производства используется два основных (определяющих) вида ресурсов S1 и S2, экономические оценки ожидаемых месячных объемов этих ресурсов составляют b1 и b2 соответственно. Например, если S1 и S2 - материальные ресурсы, то оценки b1 и b2 могут быть получены как сальдо на начало планируемого периода минус сальдо на его конец и плюс ожидаемое поступление в этом периоде согласно плану материально-технического обеспечения или согласованных предложений по финансовому плану. На предприятии имеются утвержденные в установленном порядке нормы расхода производственных ресурсов aij, i = 1, 2; j = 1, 2.
Маркетинговые исследования показали возможность сбыта любых объемов произведенной продукции по приемлемым продажным ценам – с1 и с2, соответственно (неограниченность рынка сбыта). Понятно, что в этих условиях эквивалентны два критерия оптимальности - «максимум объемов готовой продукции» и «максимум объемов реализованной продукции (выручки)».
Необходимо выбрать такой вариант месячной производственной программы, который позволил бы максимизировать выручку от продажи готовой продукции. Численные значения приведенных выше величин содержатся в таблице:
| Продукция | Нормы расхода сырья, кг/ед. | Объемы запасов сырья, кг | |
|---|---|---|---|
| Сырье | Р1 | Р2 | |
| S1 | a11 = 1 | a12 = 3 | b1 = 300 |
| S2 | a21 = 1 | а22 = 1 | b2 = 150 |
| Цена продажи, у.е./ед. | С1 = 2 | С2 = 3 | ----------- |
Математическая модель задачи
Обозначим объем производства продукции Р1 – х1 (ед.), продукции Р2 — х2 (ед.). С учетом этих обозначений математическая модель задачи имеет вид:
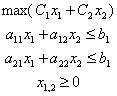 или
или
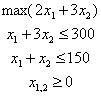
Приведенная модель является моделью типа 1а2а3а4а5а, т.е. моделью линейного программирования. Решение по этой модели — оптимальная производственная программа может быть получена симплекс-методом (см. ниже).
Выбору того или иного метода решения конкретной задачи оптимального программирования предшествует ее классификация, т.е. отнесение к одному из классов оптимизационных задач начиная с приведенных самых общих признаков.
Развитие и совершенствование методов решения задач оптимального программирования идет от случаев типа а) к случаям типа б), в).
Наиболее изученными задачами являются задачи линейного программирования (ЗЛП), для которых разработан универсальный метод решения — метод последовательного улучшения плана (симплекс-метод), т.е. любая ЗЛП решается (реализуется) этим методом.
Пакет Excel содержит программу (надстройку) Поиск решения, позволяющую реализовывать модели линейной, нелинейной и дискретной оптимизации.
Первым шагом при работе с командой (программой, надстройкой) Сервис/Поиск решения является создание специализированного листа, т.е. специальная запись ЭММ в терминах электронной таблицы (ЭТ) Excel.
Для этого необходимо создать в специальном окне диалога целевую ячейку, в которой записывается целевая функция модели, а также одну или несколько изменяемых (переменных) ячеек, которые, как правило, отвечают управляющим переменным в модели и значения которых могут изменяться для достижения экстремума (максимума или минимума) целевой функции. Для успешного поиска решения необходимо, чтобы каждая из переменных ячеек (в общем случае можно задать до двухсот таких ячеек) влияла на целевую ячейку (другими словами, формула в целевой ячейке должна опираться в вычислениях на значения переменных ячеек). В противном случае при выполнении команды Поиск решения появляется сообщение об ошибке Результаты целевой ячейки не сходятся.
Ограничения модели определяются с помощью значений соответствующих ячеек, которые должны находиться в определенных пределах или удовлетворять граничным условиям. Ограничения могут налагаться как на целевую, так и на переменные ячейки (по два ограничения для каждой изменяемой ячейки с указанием верхнего и нижнего пределов, а также до ста дополнительных). Таким образом, на специализированном листе должны содержаться ячейки, в которых вычисляются ограничиваемые величины. Тип каждого из ограничений модели (≤, =, ≥) задается (вводится) в специальном окне диалога при выполнении команды Поиск решения. Численные значения самих ограничений включать в специализированный лист необязательно; они также вводятся в специальном окне диалога при выполнении команды Поиск решения.
После команды Выполнить диалогового окна Поиск решения осуществляется поиск оптимального решения: в итоге появляется диалоговое окно Результаты поиска решения.
В режиме Справки этого диалогового окна содержатся сведения об итоговых сообщениях процедуры поиска решения. Например, в случае несовместности системы ограничений Excel будет выдавать сообщение Поиск не может найти подходящего решения. Если же решение задачи отсутствует вследствие неограниченности целевой функции на множестве допустимых решений, то Excel будет выдавать сообщение Значения целевой ячейки не сходятся. При успешном завершении решения задачи появляется диалоговое окно Результат поиска решения. Решение найдено. С помощью рубрики Результаты этого диалогового окна можно получить отчет по результатам решения [4, 8].