Тема 1. Оптимизационные экономико-математические модели
Тема 2. Методы получения оптимальных решений
Тема 4. Методы и модели анализа экономических процессов
Тема 5. Прогнозирование экономических процессов с использованием временных рядов
Тема 6. Производственные функции
Тема 7. Методы и модели управления и принятия решений в экономических системах
Тема 3. Балансовые модели
Балансовый метод планирования, матричные модели. Экономико-математическая модель межотраслевого стоимостного баланса, определение объемов валовой и конечной продукции. Матрица коэффициентов прямых материальных затрат, ее продуктивность. Матрица коэффициентов полных материальных затрат, способы ее определения. Межпродуктовый баланс. Динамическая модель межотраслевого баланса. Примеры использования матричных моделей, сведения о компьютерной реализации.
Матричные (балансовые) модели представляют собой математическое выражение балансового метода планирования (метод взаимного сопоставления затрат и результатов).
Матричные модели объединяют общий принцип построения, единство системы расчетов и аналогичность ряда экономических характеристик.
В качестве примера указанных моделей в данной теме рассматриваются статическая и динамическая модели межотраслевого стоимостного баланса, межпродуктовый баланс для обеспечения взаимоувязки планов производства группы предприятий или обособленных подразделений (цехов, иных структур) одной организации.
Основное внимание при этом уделяется структуре и экономической интерпретации элементов статических моделей.
Межотраслевой баланс отражает производство и распределение валового национального продукта по отраслям, межотраслевые потоки, использование материальных и трудовых ресурсов, создание и распределение национального дохода [1].
ЭММ межотраслевого баланса представляет собой систему уравнений, отражающих функциональную взаимосвязь включенных в его систему элементов:
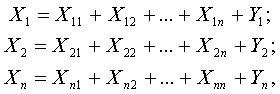
где Х = (Х1, Х2, ..., Хn) — вектор валовой продукции,
Y = (Y1, Y2, ..., Yn) — вектор конечной продукции (конечное потребление и накопление),
Хij — производственные (материальные) затраты j-й отрасли продукции i-и отрасли в течение планового периода, допустим, года (например, если отрасль 1 — угольная, отрасль 2 - черная металлургия, то X12 — годовые затраты угля на производство черных металлов).
С учетом обозначений
aij = Xij / Xj; Xij = aijXj
система уравнений перепишется в виде
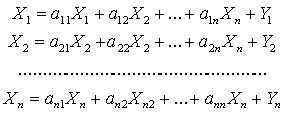
или в более компактном виде:
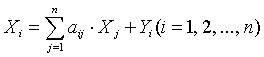
(запись с использованием знаков суммирования), X = АХ+Y, А = (aij)n*n (запись в матричной форме).
Именно, в этих двух формах записи, как правило, и используется ЭММ межотраслевого баланса, которую называют моделью Леонтьева или моделью «затраты-выпуск».
Элементы aij матрицы А называют коэффициентами прямых (материальных) затрат - это затраты i-и отрасли на единицу (рубль) валовой продукции j-й отрасли.
В матричной форме модель Леонтьева можно записать в виде X - АХ = Y или (Е - А)X = Y.
Последнее соотношение можно использовать для анализа и планирования для решения следующих задач:
1) определение объемов конечного продукта отраслей Y1, Y2, ..., Yn по заданным объемам валовой продукции (Е - А)Х = Y;
2) определение объемов валовой продукции отраслей Х1, Х2, ..., Хn по заданным объемам конечной продукции: Х = (E - A)-1×Y; X = BY, В = (Е - А)-1.
Кроме того, можно определить величины конечной продукции части отраслей и объемы валовой продукции других отраслей, если задать для первых отраслей величины валовой продукции, а для всех остальных отраслей задать объемы конечной продукции.
Элементы bij обратной матрицы В = (Е-А)-1 называются коэффициентами полных (материальных) затрат - это затраты i-й отрасли на каждый рубль конечной продукции отрасли j.
Соответственно матрицу В называют матрицей коэффициентов полных затрат, а матрицу А - матрицей коэффициентов прямых затрат.
Неотрицательную матрицу А (А ≥ 0) называют продуктивной, если существует хотя бы один такой положительный вектор X > 0, что (Е - А) X > 0.
Это определение имеет простой экономический смысл: матрица А продуктивна, если существует такой план X > 0, что каждый объект (отрасль, предприятие, цех) может произвести некоторое количество конечной продукции.
Имеет место замечательный факт, что продуктивность матрицы А ≥ 0 является необходимым и достаточным условием существования, единственности и неотрицательности решения системы уравнений Y = (Е - А) X при любом неотрицательном векторе Y ≥ 0.
Укажем некоторые способы определения продуктивности матрицы А (признаки продуктивности): для ее продуктивности необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий.
1. Матрица (Е — А) неотрицательно обратима, т.е. существует обратная матрица (Е - А)-1 и все ее элементы неотрицательны.
2. Положительны все главные миноры матрицы (Е - А).
3. Матричный ряд Е + А + А2 + ... = ∑Ak сходится, причем ∑Аk = (Е - А)-1.
4. Максимальное собственное число матрицы А меньше единицы - λ(А) < 1 (собственными значениями (числами) квадратной матрицы А называются корни (решения) характеристического уравнения |A - λЕ| = 0).
Пример 1. Оценить продуктивность матрицы
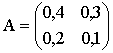 .
.
Решение. Оценку произведем по второму и четвертому признакам.
1. Рассмотрим матрицу 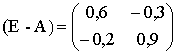 .
.
Определим ее главные миноры: Δ1 = 0,6 > 0; Δ2 = 0,54 - 0,06 = 0,48 > 0. Таким образом, матрица А - продуктивна.
Рассмотрим характеристическое уравнение |А — λЕ| = 0:
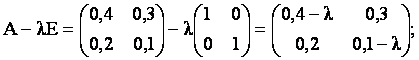
|A-λE| = (0,4 - λ)(0,1 - λ) – 0,06 = λ2 - 0,5λ - 0,02 = 0;
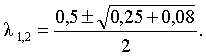
Таким образом,
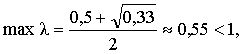
следовательно, матрица А продуктивна.
Рассмотрим межпродуктовую балансовую модель на примере предприятия, у которого в каждом цехе производится только один вид продукции в объеме Xi (i = 1, ..., n). Отдельный вид продукции может быть использован как промежуточный продукт, идущий на внутреннее потребление (передаваемый другим цехам), и как конечный продукт, поступающий непосредственно потребителю.
Обозначим через Xij количество продукции i-го вида, потребляемой для изготовления j-й продукции в количестве Xj; через Yi - выпуск конечной продукции i-го вида.
Общий (валовый) выпуск продукции i-го вида (потребность в ее производстве) равен сумме промежуточного и конечного продукта:
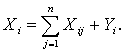
Обозначим через аij = Хij / Хj норму расхода продукции i-го вида на производство продукции j-го вида, т.е. в принятой интерпретации это коэффициент прямых затрат. Тогда
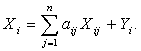
Эта система балансовых уравнений в матричной форме имеет вид:
X = АХ + Y.
Используя приведенное матричное уравнение, можно найти:
1) валовый выпуск продукции путем умножения матрицы коэффициентов полных затрат на вектор конечной продукции:
X = (E - A)-1Y;
2) распределение продукции между цехами путем умножения коэффициентов прямых затрат на общий выпуск:
Xij = aijXj.
Пример 2. Предприятие выпускает продукцию трех видов, причем каждое из его структурных подразделений (цехов) специализируется на выпуске только одного вида: первый цех выпускает продукцию первого вида, второй - продукцию второго вида, третий - продукцию третьего вида. Часть продукции идет на внутреннее потребление, остальная является конечным продуктом.
Имеются экономические оценки коэффициентов прямых затрат и объемов конечной продукции:
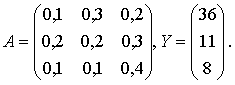
Требуется составить баланс производства и распределения продукции предприятия.
Решение. Модель баланса производства и распределения продукции предприятия можно представить следующей системой уравнений:
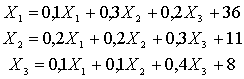
Отсюда определяем валовую продукцию цехов (студентам необходимо уметь решать системы уравнений методом Жордана-Гаусса и методом обратной матрицы):
X1 = 60, X2 = 40, X3 = 30.
Распределение продукции между цехами на внутреннее потребление определяем из соотношения
Xij = aijXj, т.е. X11 = 0,1*60 = 6; X12 = 0,3*40 = 12 и т.д.
В итоге плановая модель — баланс производства и распределения продукции предприятия — будет иметь следующий вид (см. табл.)
| Межпродуктовый баланс производства и распределения продукции | |||||
|---|---|---|---|---|---|
| Производящие структуры | Потребляющие структуры | Конечный продукт | Валовой продукт | ||
| 1 | 2 | 3 | |||
| 1 | 6,0 | 12,0 | 6,0 | 36 | 60 |
| 2 | 12,0 | 8,0 | 9,0 | 11 | 40 |
| 3 | 6,0 | 4,0 | 12,0 | 8 | 30 |
| Итого | 24 | 24 | 27 | 55 | 130 |