2. Методические указания по выполнению практической части курсовой работы

Благосостояние любого общества определяется эффективностью экономики, выражаемой произведенным количеством продуктов и услуг. В свою очередь, для производства продуктов и услуг необходимы различные виды ресурсов (активов) - материальные, трудовые, финансовые и т.п.

Осуществляя инвестиции в подобные ресурсы, отдельные индивидуумы и общество в целом ожидают получения от своих вложений тех или иных выгод в будущем. Поэтому в процессе принятия и реализации инвестиционных решений возникает необходимость в оценке их современной и будущей стоимости, риска и доходности, текущих условий и возможных последствий и т.д.

В целом инвестиционные решения представляют собой комплексный процесс, который можно условно разбить на следующие этапы:

1. Постановка целей и выбор объектов инвестирования.

2. Оценка объектов инвестирования.

3. Принятие инвестиционного решения.

4. Реализация принятых решений.

5. Оценка эффективности результатов принятых решений.

Особую роль при этом играет инвестиционный анализ или оценка объектов будущих вложений. Глубокое понимание и освоение теоретико-методологических принципов инвестиционного анализа составляют фундаментальную основу подготовки квалифицированного специалиста в области управления финансами.

Теоретические положения и современные достижения инвестиционного анализа в значительной степени базируются на методах и моделях оценки финансовых активов. В этой связи целью настоящей работы является рассмотрение базовых принципов и методов оценки эффективности инвестиций в финансовые активы (инструменты), а также формирование практических навыков ее осуществления.

Под финансовым активом (инструментом) в широком смысле понимают любое законодательно признанное соглашение, отражающее отношения владения или займа.

Принято различать финансовые активы, не являющиеся объектом свободной купли/продажи (non-transferable) и свободно обращающиеся на рынках (transferable). К первым относятся банковские инструменты (в основном - депозиты), ко вторым - фондовые (ценные бумаги).

Доход от финансовых активов может быть получен за счет:

обещанных эмитентом выплат;
прироста стоимости вложенных средств;
и того и другого.

В развитых странах основным объектом финансовых инвестиций являются ценные бумаги. Существенное возрастание в последние десятилетия роли фондовых инструментов как объектов инвестирования получило название процесса секьюритизации (securitization).

Цена подобных активов формируется рынком и может значительно отклоняться от их номинальной стоимости. Таким образом, с одной стороны, вложения в финансовые активы характеризуются возможным получением высокой доходности, с другой - связаны с повышенным риском.

Развитие процесса секьюритизации привело к появлению самых разнообразных фондовых инструментов. Вместе с тем все они могут быть условно отнесены к одному из трех классов:

финансовые инструменты с фиксированным доходом;

финансовые инструменты с переменным доходом;

производные финансовые инструменты (деривативы).

В общем случае оценка финансовых активов сводится к решению двух основных задач: определению их «внутренней» или «справедливой» цены и доходности. В совокупности они составляют необходимый минимум критериев для принятия решений.

Существуют два основных подхода к оценке финансовых активов: технический и фундаментальный анализ. Технический анализ ориентирован на краткосрочную перспективу и проведение спекулятивных операций, поэтому он не рассматривается в дальнейшем.

Фундаментальный анализ базируется на предположении о том, что внутренне присущая или «справедливая» стоимость любого актива равна дисконтированной стоимости генерируемого им в будущем потока платежей, т.е.

V=\sum_{t=1}^n\frac{CF_t}{(1+r_t)^t},\quad\left(1\right)

где CF_t - выплата по активу в момент t;

r_t - выплата по активу в момент t.

Таким образом, решение проблемы оценки зависит от того, насколько точно удастся определить или предсказать потоки платежей, время их осуществления и ставки дисконтирования.

2.1. Оценка эффективности инвестиций в инструменты с фиксированным доходом

Среди огромного разнообразия финансовых инструментов особое место занимают ценные бумаги с фиксированным доходом (fixed income securities). Примерами подобных бумаг являются различные виды облигаций, сертификатов, векселей и других обязательств. К этому классу ценных бумаг могут быть отнесены и привилегированные акции, если по ним выплачивается фиксированный дивиденд.

Общепринятый термин «фиксированный доход», строго говоря, не следует воспринимать буквально. Он призван подчеркнуть лишь то обстоятельство, что теоретически размеры и сроки платежей по таким бумагам известны (оговорены в контракте или проспекте эмиссии), по крайней мере, на момент проведения операции.

В настоящее время существует огромное, постоянно растущее число различных видов финансовых инструментов с фиксированным доходом. Поскольку рассмотрение всех подобных инструментов в рамках одной работы не представляется возможным, основное внимание в дальнейшем будет уделено облигациям как наиболее типичному и широко распространенному в мире виду финансовых инструментов, приносящих фиксированный доход. Вместе с тем рассматриваемые ниже методы и модели оценки применимы для любых финансовых инструментов с фиксированным доходом.

Облигации являются долговыми инструментами или обязательствами (т.е. выражают отношения займа) и могут выпускаться в обращение государственными или местными органами управления, а также коммерческими предприятиями.

Несмотря на существование разнообразных видов облигаций, по форме выплаты дохода их можно разделить на:

купонные, с фиксированной или плавающей ставкой купона;

дисконтные, или облигации с нулевым купоном;

с выплатой дохода в момент погашения.

Купонные облигации, наряду с возвращением основной суммы долга, предусматривают периодические денежные выплаты. Размер этих выплат определяется ставкой купона k, выраженной в процентах к номиналу. Купонные выплаты осуществляются 1, 2 или 4 раза в год.

При фиксированном купоне денежный поток, генерируемый подобными ценными бумагами, представляет собой аннуитет, к которому в конце срока операции прибавляется дисконтированная номинальная стоимость облигации. В целях упрощения мы будем предполагать, что дисконтирование осуществляется по единой ставке r. Тогда стоимость купонной облигации можно определить по формуле

V=\sum_{t=1}^{mn}\frac{(N\times{k})/m}{(1+r/m)^t}+\frac{F}{(1+r)^{mn}},\quad\left(2\right)

где F - сумма погашения (как правило, номинал, т.е. F = N);

k - годовая ставка купона;

r - рыночная ставка (норма дисконта);

n - срок облигации;

N - номинал;

m - число купонных выплат в году.

Пример 1.

Определить текущую стоимость трехлетней облигации с номиналом в 1000,00 и годовой купонной ставкой 8%, выплачиваемых раз в квартал, если норма доходности (рыночная ставка) равна 12%.

V=\sum_{t=1}^{12}\frac{(1000\times{0,08})/4}{(1+0,12,/4)^t}+\frac{1000}{(1+0,12/4)^{12}}=900,46.

Таким образом, норма доходности в 12% по данной операции будет обеспечена при покупке облигации по цене, приблизительно равной 900,46.

Соотношение (2) представляет собой базовую основу для оценки стоимости любого финансового инструмента с периодическим фиксированным доходом и соответственно купонной облигации.

Если срок погашения купонной облигации достаточно большой, например, свыше 30 лет, для целей текущего анализа ее удобно рассматривать как бессрочную.

Стоимость бессрочной облигации может быть определена из предположения, что генерируемый ею поток платежей представляет собой вечную ренту (perpetuity). Тогда можно показать, что¹

V_\infty=\frac{CF}{r}.\quad\left(3\right)

Если платежи осуществляются m раз в год, формула исчисления стоимости вечной ренты примет следующий вид:

V_\infty=\frac{CF}{m[(1+r)^{1/m}-1]}.\quad\left(4\right)

Пример 2.

Определим текущую стоимость 100 единиц облигации фирмы IBMсо сроком обращения 100 лет, исходя из требуемой нормы доходности в 8,5%. Ставка купона равна 7,72%, выплачиваемых раз в полгода.

V_\infty=\frac{7,72/2}{2[(1,085)^{0,5}-1]}=40,35.

Процесс оценки стоимости бескупонной или дисконтной облигации заключается в определении современной величины элементарного потока платежей, по известным значениям номинала N, процентной ставки r и срока погашения n. С учетом принятых обозначений, формула текущей стоимости (цены) подобного актива примет следующий вид:

V=\frac{N}{(1+r)^n}.\quad\left(5\right)

Поскольку номинал бескупонной облигации принимается за 100%, ее курсовая стоимость равна:

K=\frac{100}{(1+r)^n}.\quad\left(6\right)

Пример 3.

Какую цену заплатит инвестор за бескупонную облигацию с номиналом в 1000,00 и погашением через три года, если требуемая норма доходности равна 4,4%?

1000/(1 + 0,044)³ = 878,80.

Облигации с нулевым купоном представляют интерес для инвесторов, проводящих операции с четко заданным временным горизонтом. Они играют важную роль в инвестиционном анализе, так как определяют временную структуру процентных ставок на рынке.

Из приведенных соотношений и примеров следует, что стоимость рассмотренных типов облигаций связана обратной зависимостью с рыночной ставкой r и сроком погашения n.

Цена долгосрочного инструмента с выплатой процентов в момент погашения равна современной стоимости генерируемого потока платежей, обеспечивающей получение требуемой нормой доходности. Пусть k - процентная ставка, обещанная к выплате. С учетом принятых обозначений, цена покупки P и курс K подобного инструмента, исходя из требуемой (рыночной) доходности, будут равны:

P=N\left(\frac{1+k}{1+r}\right)^n,\quad\left(7\right)

P=100\left(\frac{1+k}{1+r}\right)^n,\quad\left(8\right)

Из приведенных соотношений следует, что при k < r, цена (курс) инструмента будет ниже номинала (т.е. он будет продаваться с дисконтом). Соответственно если k > r, цена (курс) будет больше номинала, и он будет продаваться с премией. При этом по мере увеличения срока погашения n курсовая стоимость будет расти экспоненциально.

Пример 4.

Депозитный сертификат коммерческого банка имеет номинал 100000,00 и срок погашения 5 лет. Ставка по сертификату равна 30% годовых, начисляемых один раз. Определить стоимость обязательства, если рыночная доходность равна 35%.

P=100000\times\left(\frac{1+0,3}{1+0,35}\right)^5=82803,35.

В качестве общей меры эффективности инвестиций в облигации используется показатель доходности к погашению (Yield To Maturity - YTM).

Доходность к погашению представляет собой процентную ставку, устанавливающую равенство между текущей стоимостью потока платежей по облигации V и ее рыночной ценой P.

Для облигаций с фиксированным купоном, выплачиваемым раз в году, она определяется путем решения следующего уравнения относительно YTM:

P=\sum_{t=1}^{n}\frac{CF}{(1+YTM)^t}+\frac{F}{(1+YTM)^n},\quad\left(9\right)

где F - цена погашения (как правило, номинал N).

Уравнение решается относительно YTM каким-либо итерационным методом. Следует отметить, что вычисляемый по формуле (9) критерий YTM, по сути, представляет собой, внутреннюю норму доходности (т.е. показатель IRR) инвестиции. При этом следует обратить внимание на то, что реальная доходность облигации к погашению будет равна YTM только при выполнении следующих условий:

облигация хранится до срока погашения;

полученные купонные доходы немедленно реинвестируются по ставке r = YTM.

Таким образом, между доходностью к погашению YTM и ставкой реинвестирования купонного дохода r существует прямая зависимость. С уменьшением r будет уменьшаться и величина YTM; с ростом r величина YTM будет также расти.

На величину показателя YTM оказывает влияние и цена покупки облигации. Фундаментальная зависимость доходности к погашению YTM купонной облигации от ее рыночной стоимости P показана на рис. 1. Нетрудно заметить, что зависимость здесь обратная.

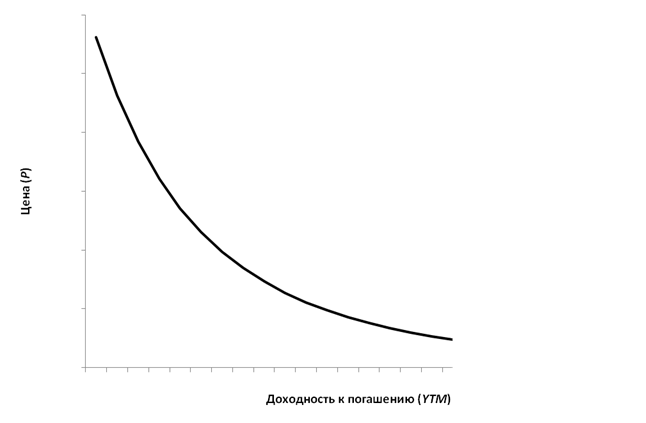
Зависимость YTM от цены

Рис. 1. Зависимость YTM от цены P

Сформулируем фундаментальные правила, отражающие взаимосвязи между ставкой купона k, доходностью к погашению YTM и ценой облигации P:

если P > N, k > YTM;
если P < N, k < YTM;
если P = N, k = YTM.

Руководствуясь данными правилами, не следует забывать о зависимости YTM от ставки реинвестирования купонных платежей. В целом, показатель YTM необходимо рассматривать как среднюю ожидаемую доходность к погашению.

Для удобства анализа доходности бессрочных облигаций делается допущение о бесконечности приносимых ими периодических доходов. Поскольку выплата номинала (погашение облигации) в обозримом будущем не ожидается, единственным источником получаемого дохода считаются купонные платежи.

Для определения доходности к погашению YTM бессрочной облигации можно использовать следующее соотношение:

YTM=\biggl[1+\frac{k}{m}\times\frac{100}{K}\biggr]^m-1,\quad\left(10\right)

где m - число купонных выплат в год.

Пример 5.

Облигация фирмы IBMсо сроком обращения 100 лет была куплена по курсу 92,50. Ставка купона равна 7,72%, выплачиваемых раз в полгода. Определить доходность операции.

YTM = (1 + (0,0772/2)(100/92,50))² - 1 ≈ 0,0852 (или ≈ 8,5%).

Как следует из полученных результатов, доходность к погашению данной облигации выше купонной.

Для бескупонной облигации единственным источником дохода является разница между ценой покупки и номиналом (ценой погашения). Поскольку номинал облигации всегда известен (или может быть принят за 100%), для определения доходности операции достаточно знать две величины - цену покупки P (либо курс K) и срок погашения n.

Тогда доходность к погашению бескупонной облигации можно определить по следующей формуле:

YTM=\sqrt[n]{\frac{N}{P}}-1=\sqrt[n]{\frac{100}{K}}-1.\quad\left(11\right)

Пример 6.

Бескупонная облигация с номиналом в 1000,00 и погашением через 3 года приобретена по цене 878,00. Определить доходность облигации к погашению.

YTM=\sqrt[3]{\frac{1000}{878,80}}-1=0,044\ \left(или\ 4,4\%\right).

Из (11) следует, что доходность бескупонной облигации YTM находится в обратной зависимости по отношению к цене P и сроку погашения n.

Для инструментов с выплатой доходов в момент погашения начисленные проценты выплачиваются одной суммой вместе с номиналом по истечении срока обращения.

Базовое соотношение для исчисления будущей стоимости FV такого потока платежей имеет следующий вид:

FV = P(1 + k)ⁿ,

или в случае m начислений в году

FV = P(1 + k/m)^mn,

где k - обещанная ставка процентного дохода;

P - текущая стоимость (как правило, цена покупки - номинал N).

Тогда доходность к погашению YTM можно определить из следующего соотношения:

YTM=\sqrt[n]{\frac{FV}{P}}-1.\quad\left(12\right)

На практике подобные инструменты могут продаваться на вторичных рынках по ценам, отличающимся от номинала. Поэтому в общем случае доходность к погашению YTM удобно выражать через цену покупки P

YTM=\frac{1+k}{\sqrt[n]{\frac{P}{N}}}-1.\quad\left(13\right)

Пример 7.

Депозитный сертификат коммерческого банка номиналом в 100 000,00 со сроком погашения через 5 лет был приобретен за 95000,00. Ставка по сертификату равна 30% годовых. Определить доходность инвестиции.

YTM=\frac{1+0,3}{\sqrt[5]{\frac{95000}{100000}}}-1=0,3134.

Из (13) следуют следующие правила взаимосвязи доходности к погашению и рыночной стоимости (курса) подобного инструмента:

если P < N (K < 100), то YTM > k;
если P = N (K = 100), то YTM = k;
если P > N (K > 100), то YTM < k.

До сих пор мы принимали во внимание только одну временную характеристику облигаций - срок погашения n. Однако для обязательств с выплатой периодических доходов не менее важную роль играет еще один временной показатель - эффективный средний срок погашения (средняя продолжительность платежей), или дюрация (duration).

Понятие «дюрация» было впервые введено американским ученым Ф.Маколи (F.R.Macaulay) и играет важнейшую роль в анализе долгосрочных активов с фиксированным доходом. В целях упрощения будем предполагать, что купонный платеж осуществляется раз в год. Тогда дюрацию D можно определить из следующего соотношения:

D=\frac{\sum_{t=1}^n{\frac{tCF_t}{(1+r)^t}+\frac{nF}{(1+r)^n}}}{\sum_{t=1}^n{\frac{CF_t}{(1+r)^t}+\frac{F}{(1+r)^n}}},\quad\left(14\right)

где CF_t - величина платежа по купону в периоде t;

F - сумма погашения (как правило, номинал);

n - срок погашения;

r - процентная ставка (норма дисконта), равная доходности к погашению (r = YTM).

Нетрудно заметить, что дюрация является средневзвешенной из периодов поступлений по облигации. Используемые при этом веса представляют собой долю каждого дисконтированного платежа в современной стоимости всего потока.

Как следует из (14), дюрация зависит от трех факторов: ставки купона k, срока погашения n и доходности YTM. Эта зависимость для 20-летней облигации при различных ставках k и YTM показана рис. 2.

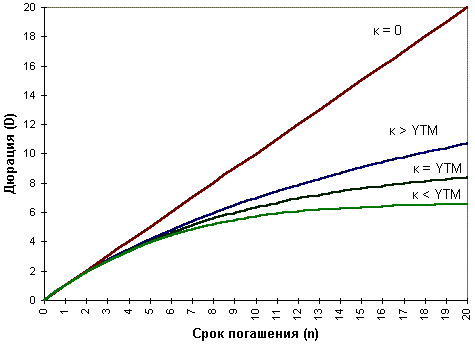
Зависимость дюрации от показателей k и YTM

Рис. 2. Зависимость дюрации от показателей k и YTM

Графическая иллюстрация взаимосвязи дюрации с показателями n, k и YTM позволяет сделать ряд важных выводов:

дюрация облигации с нулевым купоном всегда равна сроку ее погашения, т.е. при k = 0, D = n;
дюрация купонной облигации всегда меньше срока погашения: при k > 0, D < n;
с ростом доходности (процентной ставки на рынке) дюрация купонной облигации уменьшается и наоборот.

Показатель дюрации, или средней продолжительности, более корректно учитывает особенности временной структуры потока платежей. Как следует из (14), отдаленные платежи имеют меньший вес и, следовательно, оказывают меньшее влияние на результат, чем более близкие к моменту оценки.

Дюрацию часто интерпретируют как средний ожидаемый срок платежей или погашения обязательства с учетом его современной стоимости. В частности, дюрацию купонной облигации можно трактовать как срок эквивалентного обязательства без текущих выплат процентов (например, облигации с нулевым купоном).

Другая интерпретация дюрации - средний срок, в течение которого средства связаны в активе с фиксированным доходом (т.е. срок окупаемости данной инвестиции).

Вернемся еще раз к формуле (14). Обозначим отношение дисконтированного платежа к дисконтированной стоимости всего потока в конкретный момент времени t через w_t, т.е.

w_t=\frac{\frac{CF_t}{(1+YTM)^t}}{PV}.

Тогда (14) примет следующий вид:

D=\sum_{t=1}^n{tw_t}.\quad\left(15\right)

В полученном соотношении величины w_t выполняют роль удельных весов для соответствующих моментов времени, показывая их вклад в современную стоимость потока платежей. При этом величины w_t не могут быть отрицательными. Нетрудно показать, что их сумма всегда равна 1:

\sum_{t=1}^n{w_t}=1.

Эти свойства весов w_t позволяют условно трактовать их как вероятности, а формулу (15) и дюрацию - как математическое ожидание срока погашения обязательства.

Однако главная ценность дюрации состоит в том, что она приблизительно характеризует чувствительность цены облигации к изменениям процентных ставок на рынке (доходности к погашению). Таким образом, используя дюрацию, можно управлять риском, связанным с изменением процентных ставок.

В общем случае, процентный риск облигации может быть измерен показателем эластичности ее цены P по отношению к рыночной ставке r.

Если r = YTM, то можно показать, что:

\frac{\Delta P}{P}=-D\biggl[\frac{\Delta YTM}{1+YTM}\biggr].\quad\left(16\right)

В расчетах более удобно использовать показатель модифицированной дюрации (modified duration - MD):

MD=\frac{D}{1+YTM}.\quad\left(17\right)

Тогда

\frac{\Delta P}{P}=-(MD\times\Delta YTM).\quad\left(18\right)

Формулу (18) часто используют для определения приблизительного изменения цены облигации исходя из предполагаемого изменения доходности к погашению.

Пример 8.

Предположим, что облигация номиналом в 1000 руб. из примера со сроком погашения 3 года и ставкой купона 1% куплена по номиналу. При этом инвестор ожидает рост рыночной процентной ставки на 1 %. Определить ожидаемое изменение цены облигации при условии, что ее дюрация равна 2,8.

Определим ожидаемое процентное изменение YTM:

ΔYTM = 0,01/(1 + 0,07) = 0,0093.

Найдем величину MD:

MD = 2,8/0,0093 = 2,62.

Предполагаемое процентное изменение цены облигации составит

ΔР = -(0,01 × 2,62)= -0,0262 ≈ -2,6%.

Таким образом, курс облигации должен понизиться на 2,6%. Поскольку облигация была куплена по номиналу, новый курс должен быть приблизительно равен: 100 - 2,6 = 97,4%.

Осуществим проверку нашего предположения (т.е. определим курс облигации, при условии, что YTM = 8%):

P=\sum_{t=1}^3\frac{1000\times0,07}{(1+0,08)^t}+\frac{1000}{(1+0,08)^3}=974,23;

K=\frac{P}{N}100=\frac{974,23}{1000}100=97,42\approx97,4.

Завершая рассмотрение свойств дюрации, кратко остановимся на недостатках, присущих данному показателю.

Первое ограничение вытекает из нелинейной формы связи между YTM и P(см. рис. 1). Поскольку скорость изменения показателей при этом будет разной, применение показателей D или MD для прогнозирования цен облигаций в случае значительных колебаний процентных ставок будет приводить к преувеличению падения курса при росте YTM и занижению реального роста курса при уменьшении YTM.

Другим существенным недостатком дюрации как меры измерения процентного риска является неявное допущение о независимости доходности от срока погашения. Таким образом, предполагается, что краткосрочные процентные ставки изменяются так же, как и долгосрочные. Например, если доходность по 3-месячным ГКО изменилась на 1%, то и доходность 15-летних ОВВЗ также должна измениться на 1%. Нереалистичность подобного допущения очевидна.

Несмотря на отмеченные недостатки, показатель средней продолжительности платежей (дюрация) широко используется в теоретическом и прикладном анализе.

Как было показано выше, причинами проблем, возникающих при использовании дюрации, является нелинейность взаимосвязи между ценой и доходностью. В качестве ее характеристики используется показатель выпуклости кривой «цена-доходность», вычисляемый по формуле

C=\left(\frac{1}{P(1+YTM)^2}\right)\sum_{t=1}^n{(t^2+t)}\frac{CF_t}{(1+YTM)^t}.\quad\left(19\right)

Из (19) следует, что выпуклость прямо зависит от срока погашения n и дюрации соответственно. Можно также показать, что выпуклость является возрастающей функцией от последней. В целом, свойства выпуклости по отношению к n и k аналогичны свойствам дюрации.

Вместе с тем выпуклость связана положительной зависимостью с изменениями процентных ставок (доходности к погашению). Объяснение данного свойства следует из того факта, что выпуклость можно определить как разность между фактической ценой облигации и ее ценой, определенной с использованием модифицированной дюрации. Более удобную интерпретацию этого факта можно получить из (15). Если считать веса w_t вероятностями, то выпуклость можно рассматривать как дисперсию среднего срока погашения обязательства. При этом (19) можно переписать в виде

C=\sum_{t=1}^{n}{w_t(t-D)^2}.\quad\left(20\right)

Отсюда следует, что чем больше выпуклость (разброс), тем больше кривизна графика «цена - доходность» (см. рис. 1).

Совместное использование дюрации и выпуклости при анализе активов с фиксированным доходом позволяет существенно повысить точность оценки изменений их стоимости. Например, более эффективную формулу для определения будущей цены облигации в зависимости от изменений доходности можно задать в следующем виде:

P=P_0+(P_0\times D\times \partial(YTM))+\left(\frac{1}{2}\times P_0\times C\times \partial(YTM)^2\right),\quad\left(21\right)

где P - будущая цена при условии, что доходность изменится на величину ∂(YTM);

P₀ - текущая цена;

D - дюрация;

С - выпуклость.

Рассмотренные свойства количественных характеристик облигаций являются теоретической базой для разработки моделей управления портфелями ценных бумаг с фиксированным доходом. В частности, они широко используются для балансировки активов и обязательств, хеджирования портфелей от процентного риска.

Можно сформулировать следующие правила хеджирования процентного риска.

Для базовой ставки процента r текущая стоимость актива должна быть равна текущей стоимости долга: PV(Актив) = PV(Долг).
Для базовой процентной ставки r дюрация актива должна совпадать с дюрацией долга: D(Актив) = D(Долг).
Выпуклость актива должна быть больше выпуклости долга: С( Актив) > С(Долг).

Выполнение двух первых правил приводит к так называемому неполному хеджированию. Этот способ, разработанный известным экономистом П.Самуэльсоном, называют иммунизацией (immunization). При этом портфель становится нечувствительным к небольшим изменениям процентной ставки.

Выполнение третьего правила приводит к полному хеджированию. В таблице и на рис. 3 приведены пример расчета и графическая интерпретация механизма полного хеджирования 10-летнего обязательства «В», взятого под 12% годовых, специально подобранным активом «А». Актив и долг имеют одинаковую текущую стоимость PV дюрацию D, но разную выпуклость С. Таким образом, их графики «цена - доходность» имеют общую точку с координатами (r₀, PV₀), через которую проходит и общая касательная (линия дюрации). Однако выпуклость кривой «цена - доходность» актива больше, чем у аналогичной кривой обязательства. Поэтому независимо от изменения рыночной ставки процентов разность стоимостей актива и обязательства всегда неотрицательная: PV(A) - PV(B) ³ 0.

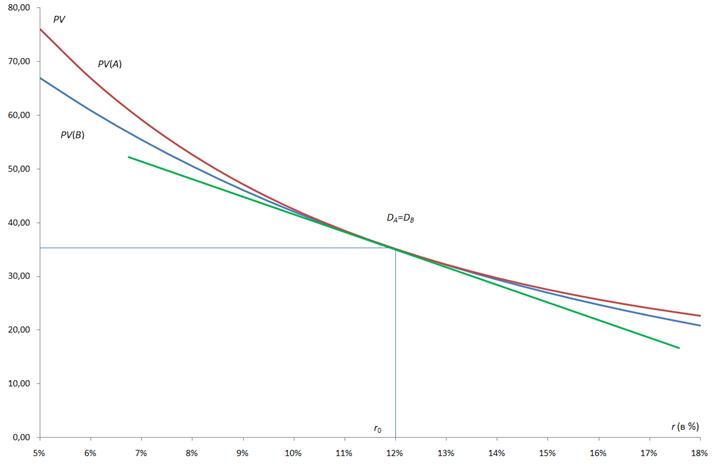
Полное хеджирование активом «А» долга «В»
(графическая интерпретация)

Рис. 3. Полное хеджирование активом «А» долга «В» (графическая интерпретация)

Детальное исследование различных характеристик подобных активов, а также технику их исчисления и моделирования в среде MS EXCEL можно найти в списке рекомендуемой литературы [2, 3, 4].

На рис. 4 приведен фрагмент электронной таблицы, содержащий полный анализ облигации внутреннего валютного займа МФ РФ.

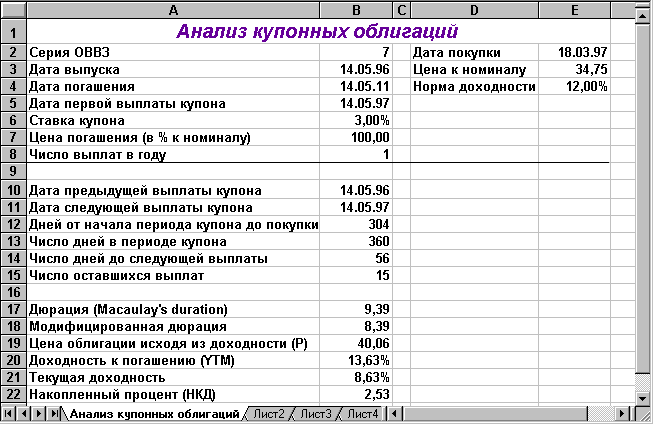
Анализ ОВВЗ МФ РФ седьмого транша

Рис. 4. Анализ ОВВЗ МФ РФ седьмого транша

*Таблица*. **Полное хеджирование активом «А» долга «В» взятого на 10 лет под 12% с единовременным погашением**
Процентная ставка	PV(B)	PV(A)	Дюрация В	PV(A) - PV(B)
0,05	66,92	76,05	13,80	9,13
0,06	60,86	66,88	13,32	6,02
0,07	55,41	59,16	12,80	3,75
0,08	50,49	52,65	12,27	2,16
0,09	46,04	47,14	11,71	1,10
0,10	42,02	42,46	11,15	0,44
0,11	38,39	38,49	10,58	0,10
0,12	35,09	35,09	10,00	0,00
0,13	32,11	32,19	9,44	0,08
0,14	29,40	29,69	8,88	0,29
0,15	26,94	27,54	8,34	0,60
0,16	24,71	25,68	7,81	0,97
0,17	22,68	24,07	7,32	1,39
0,18	20,83	22,66	6,84	1,83

2.2. Оценка эффективности инвестиций в инструменты с переменным доходом

Инструменты с переменным или неопределенным доходом представляют собой наиболее сложный и вместе с тем распространенный класс объектов инвестирования. Характерным примером подобных активов являются долевые бумаги - обыкновенные акции, паи и т.п.

Акция представляет собой ценную бумагу, удостоверяющую право собственности на определенную долю капитала и прибыли предприятия.

Несмотря на то, что техника оценки облигаций и акций базируется на единой модели дисконтирования потоков платежей, определить стоимость и доходность последних значительно сложнее в силу двух обстоятельств:

денежные выплаты (дивиденды) по акциям не гарантированы и, как правило, неизвестны заранее;
акции не имеют срока погашения.

Доход держателя акции складывается из полученных дивидендов и изменения ее рыночной стоимости. В случае однопериодной инвестиции (n = 1) стоимость акции может быть определена следующим образом:

V=\frac{DIV_1}{1+r}+\frac{P_1}{1+r},\quad\left(22\right)

где DIV₁, Р₁ - дивиденд и цена акции в периоде t = 1.

Соответственно доходность инвестиции Y будет равна

V=\frac{DIV_1+(P_1-P_0)}{P_0},\quad\left(23\right)

где P₀ - цена акции в периоде t = 0.

Для инвестиции сроком n-периодов

V=\sum_{t=1}^n\frac{DIV_t}{(1+r)^t}+\frac{P_n}{(1+r)^n}.\quad\left(24\right)

Поскольку срок обращения акции формально не ограничен, при n → ∞ последнее слагаемое в (24) будет стремиться к нулю. Тогда

V=\sum_{t=1}^{\infty}\frac{DIV_t}{(1+r)^t}.\quad\left(25\right)

Полученное выражение известно как модель дисконтирования дивидендов (DDM), которая впервые была предложена американским ученым Д.Уильямсом (J.Williams).

Согласно данной модели, стоимость обыкновенной акции равна сумме всех дивидендов, дисконтированных к текущему моменту.

Если рыночная цена акции на текущий момент известна, ее внутренняя доходность Y может быть определена из следующего уравнения:

P=\sum_{t=1}^{\infty}\frac{DIV_t}{(1+Y)^t}=0.\quad\left(26\right)

Уравнение (26) решается относительно Y каким-либо итерационным методом. Как и в случае с облигациями, величина Y представляет собой критерий внутренней нормы доходности IRR для потока платежей, генерируемых обыкновенными акциями.

Нетрудно заметить, что практическое применение (25) и (26) для оценки эффективности инвестиций в акции ограничено, прежде всего, из-за сложности определения значений величин DIV_t, поскольку инвесторы не могут точно знать, какими будут дивиденды даже в ближайшем будущем.

Поэтому при проведении анализа обычно исходят из тех или иных предположений о возможных или ожидаемых темпах роста дивидендов.

Наиболее простое предположение состоит в том, что размер дивидендов остается неизменным на протяжении всего срока инвестиции, т.е.

DIV₀ = DIV₁ =... = DIV_n = DIV = const.

Тогда стоимость акции равна

V=DIV\biggl[\sum_{t=1}^{\infty}\frac{1}{(1+r)^t}\biggr].

Поскольку при n → ∞ величина в квадратных скобках стремится к r, модель оценки примет следующий вид:

V=\frac{DIV}{r}.\quad\left(27\right)

Выражение (27) известно как модель нулевого роста Д.Гордона (J.Gordon) и может быть также использовано для оценки привилегированных акций с фиксированным дивидендом.

Пример 9.

Рыночная цена акции с ежегодным дивидендом 6,00 равна 35,00. Определить стоимость акции, если норма доходности для инвестора составляет 20%.

V=\frac{6}{0,2}=30.

Таким образом, акция является переоцененной и при прочих равных условиях от ее приобретения следует отказаться.

Доходность инвестиции в модели нулевого роста будет равна

V=\frac{DIV}{P}.\quad\left(28\right)

Для предыдущего примера внутренняя доходность акции равна 6/35 = 0,1714, что меньше требуемой нормы на 20%. Таким образом, предыдущий вывод о невыгодности операции подтверждается и этим критерием.

Еще одним простым и достаточно популярным подходом к оценке акций является модель постоянного роста.

В основе данной модели лежит допущение, что дивидендные выплаты по акции увеличиваются пропорционально некоторой величине g (т.е. с одинаковым темпом роста). Тогда

DIV_t = DIV_t-1(1 + g) или DIV_t = DIV₀(l + g)^t.

Стоимость акции при этих условиях можно определить как

V=\sum_{t=1}^{\infty}\frac{DIV_0(1+g)^t}{(1+r)^t}=DIV_0\biggl[\sum_{t=1}^{\infty}\frac{(1+g)^t}{(1+r)^t}\biggr].

Можно показать, что при n → ∞ выражение в квадратных скобках при r > g будет стремиться к величине²: (1 + g)/(r - g).

Тогда модель постоянного роста примет следующий вид:

V=DIV_0\biggl[\frac{1+g}{r-g}\biggr].\quad\left(29\right)

Пример 10.

Пусть в предыдущем примере предполагается, что ожидается постоянный рост дивидендов 5% в год. Определить стоимость акции при тех же прочих условиях.

V=6\times\biggl[\frac{1+0,05}{0,2-0,05}\biggr]=25,20.

Нетрудно заметить, что модель нулевого роста (27) является частным случаем модели постоянного роста (29), при g = 0.

Доходность инвестиции в модели постоянного роста можно определить как

Y=\frac{DIV_0(1+g)}{P}+g=\frac{DIV_1}{P}+g.\quad\left(30\right)

Если в предыдущем примере рыночная цена акции равна 35,00, при неизменных остальных данных ее доходность составит

Y=\frac{6\times(1+0,05)}{35}+0,05=0,23.

Наиболее общим и приближенным к реальности видом моделей дисконтирования дивидендов являются модели переменного роста. При этом предполагается, что до некоторого момента времени T изменения дивидендов не связаны с какой-то закономерностью. Однако после наступления момента T они будут расти с постоянным коэффициентом g.

Таким образом, инвестор должен осуществить прогноз значений дивидендов DIV₁, DIV₂, ..., DIV_T, а также периода Т. Поток выплат по акции в этом случае можно разделить на две части: до и после момента Т. Соответственно ее стоимость V будет равна сумме стоимостей двух потоков платежей: V = V_T + V_{T + l}.

Величина V_T в данном случае представляет собой сумму дисконтированных по заданной ставке r дивидендных выплат, поступивших за период Т. Поскольку предполагается, что поток платежей после момента Т изменяется с постоянным коэффициентом, его стоимость V_{T + 1} может быть определена по модели постоянного роста (29).

Тогда стоимость акции V может быть определена как

V=V_T+V_{T+1}=\sum_{t=1}^T\frac{DIV_t}{(1+r)^t}+\frac{DIV_{T+1}}{(r-g)(1+r)^T}.\quad\left(31\right)

Можно показать, что модель постоянного роста является частным случаем (31), при T = 0.

Вычисление внутренней доходности инвестиции по модели переменного роста представляет определенные сложности и осуществляется путем решения относительно Y следующего уравнения:

P=\sum_{t=1}^T\frac{DIV_t}{(1+Y)^t}+\frac{DIV_{T+1}}{(Y-g)(1+Y)^T}.\quad\left(32\right)

Современные компьютеры и соответствующие пакеты прикладных программ позволяют быстро и эффективно определить данный показатель.

Как уже отмечалось, применение модели переменного роста предполагает, что инвестор в состоянии осуществить прогноз дивидендов до наступления момента Т. Однако в реальности точно определить даже ближайшие дивидендные выплаты достаточно сложно. В этой связи в теории и практике финансового менеджмента широкое распространение получили такие частные случаи моделей переменного роста, как 2- и 3-этапные модели.

В двухэтапной модели предполагается, что в первые периоды (этап интенсивного роста) рост дивидендных выплат будет осуществляться с коэффициентом g₁, после чего наступает период стабилизации (зрелости) и рост дивидендных выплат стабилизируется на уровне g₂ (рис. 5).

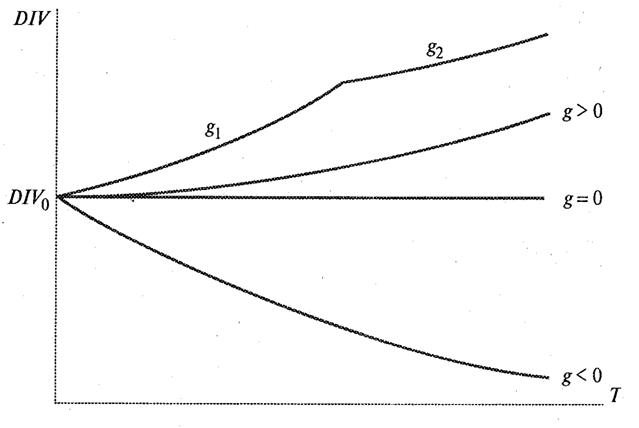
Двухэтапная модель роста дивидендов

Рис. 5. Двухэтапная модель роста дивидендов

Пример 11.

Предположим, что по акции «А» ожидают 25%-ный рост дивидендных выплат в течение следующих двух периодов, после чего он стабилизируется на уровне 5% в год. В текущем периоде дивидендные выплаты составили 2,00. Требуемая ставка доходности равна 12%. Определить стоимость акции «А».

Применив (31), получим

V=V_T+V_{T+1}=\left(\frac{2(1+0,25)}{(1+0,12)}+\frac{2(1+0,25)^2}{(1+0,12)^2}\right)+\frac{2(1+0,25)^2(1+0,05)}{(0,12-0,05)(1+0,12)^2}=4,72+37,36=42,08.

Наиболее популярной является так называемая трехэтапная модель, в которой предполагается, что аналогично понятию жизненного цикла продукта все предприятия проходят три этапа развития: этап роста, переходный этап и этап зрелости. Каждый этап характеризуется соответствующими темпами роста доходов и дивидендов. В общем случае, на первом этапе при успешном развитии предприятия рост дивидендных выплат g₁ может превышать среднеотраслевой либо, наоборот, быть довольно низким. Затем в течение некоторого переходного периода происходит стабилизация развития предприятия. Дивиденды в этом периоде могут быть относительно стабильными либо незначительно изменяться с коэффициентом g₂. После вступления в фазу зрелости дивиденды стабилизируются на некотором уровне либо растут с небольшим темпом g₃ Таким образом, в соответствии с этапами развития предприятия необходимо осуществить прогноз значений коэффициентов роста дивидендных выплат g₁, g₂, g₃, а также длительность каждого этапа. Хотя на практике трудно рассчитывать на высокую точность подобных прогнозов, разработанная модель может вполне адекватно описывать реальный процесс развития предприятия.

Рассмотренные выше разновидности моделей DDM базируются на прогнозе ожидаемых дивидендов и темпов их роста. Другим широко применяемым подходом к оценке акции является использование финансовых коэффициентов.

Наиболее простой метод подобной оценки заключается в следующем. Сначала оценивается доход на акцию в будущем периоде, т.е. определяется коэффициент EPS. Затем полученный показатель умножается на коэффициент цена/прибыль - Р/Е (фактически P/EPS), рассчитанный для аналогичных предприятий либо характерный для данной отрасли. Таким образом

V_t = EPS_t × P_t/EPS_t. (33)

На практике для расчета часто берутся текущие значения данных коэффициентов.

Величина показателя EPS в (33) может быть представлена как отношение коэффициентов дивиденда на акцию (DPS) и дивидендных выплат (payout ratio - PR):

EPS_t=\frac{DPS_t}{PR_t}.

В свою очередь, коэффициент дивидендных выплат определяется как 1 - RR, где RR - доля прибыли, реинвестированной в предприятие. Тогда

DPS_t = EPS_t × (1 - RR_t).

Это соотношение может быть переписано как

DIV_t = EPS_t(1 - RR_t). (34)

Таким образом, прогнозируя показатели EPS и Р/Е, по сути, аналитик неявно производит оценку будущих дивидендных выплат.

Выразив показатель дивидендов в модели DDM показателях доходности, используемых в (34), получим следующую формулировку:

V=\sum_{t=1}^{\infty}\frac{EPS_t(1-RR_t)}{(1+r)^t}.\quad\left(35\right)

Предприятие может использовать нераспределенную прибыль на выкуп акций или реинвестировать для получения дохода на собственный капитал, измеряемый ROE. Реинвестированная прибыль используется для финансирования внутреннего роста с темпом g = RR × ROE.

Таким образом, EPS_t = EPS₀ × (1 + g)^t = EPS₀ × (l + (RR)(ROE))^t.

Прибыльные предприятия могут обеспечить ROE > 0, реинвестируя всю нераспределенную прибыль в доходные проекты или в покупку собственных акций. Выкуп акций увеличивает EPS, поскольку прибыль в дальнейшем будет распределяться на меньшее их число. Если величина RR > 0, то следующие соотношения эквивалентны:

DIV_t = (l - RR)EPS_l.

DIV_t = (l - RR)(1 + g)^tEPS₀.

DIV_t = (l - RR)(1 + (RR)(ROE))^tEPS₀.

Выразим дивиденды в DDM через соответствующие коэффициенты

V_0=\sum_{t=1}^{\infty}\frac{(1-RR)[1+RR\times{ROE}]^t\times{EPS_0}}{(1+r)^t}.\quad\left(36\right)

Таким образом, любая разновидность DDM может быть представлена в терминах доходности, через соответствующие коэффициенты.

Многие аналитики используют показатели EPS и Р/Е для определения стоимости акций. В частности, этот подход может быть использован, даже если предприятие не платит дивидендов (путем расчета показателя PR), он прост и удобен в применении.

Используя оба подхода (метод коэффициентов и DDM), можно повысить точность оценки. В идеале оба метода должны давать одинаковый результат.

Более сложные модели оценки обыкновенных акций (вероятностная DDM, CAPM, APT, BARRA и др.) учитывают связанные с ними риски и базируются на математическом аппарате статистического, факторного, стохастического и других видов анализа.

Рассмотренные выше методы оценки финансовых активов (облигаций и обыкновенных акций), несмотря на условность лежащих в их основе допущений (отсутствие риска, инфляции, налогов, неизменность ставок дисконтирования и коэффициентов роста и т.д.), являются фундаментальной основой теории инвестиций, на которой, в свою очередь, базируются современные модели управления портфелем ценных бумаг.

1 Доказательство этой формулы можно найти в списке литературы [2, 4].

2 При g → r цена акции будет неограниченно большой.

уход за лицом

Пользователь, раз уж ты добрался до этой строки, ты нашёл тут что-то интересное или полезное для себя. Надеюсь, ты просматривал сайт в браузере Firefox, который один правильно отражает формулы, встречающиеся на страницах. Если тебе понравился контент, помоги сайту материально. Отключи, пожалуйста, блокираторы рекламы и нажми на пару баннеров вверху страницы. Это тебе ничего не будет стоить, увидишь ты только то, что уже искал или ищешь, а сайту ты поможешь оставаться на плаву.