Тема 1. Введение. Эконометрика и эконометрическое моделирование
Тема 3. Парная регрессия и корреляция
Тема 4. Модель множественной регрессии
Тема 5. Системы линейных одновременных уравнений
Тема 6. Многомерный статистический анализ
Задание для выполнения контрольной работы по дисциплине «Эконометрика»
Задание для выполнения лабораторной работы. Задачи для ЭВМ (СТАТЭКСПЕРТ)
Тема 4. Модель множественной регрессии
Линейная модель множественной регрессии имеет вид:
Yi = α0 + α1xi1 + α2xi2 + ... + α mxim + εi (4.1)
Коэффициент регрессии αj показывает, на какую величину в среднем изменится результативный признак Y, если переменную xj увеличить на единицу измерения, т.е. αj является нормативным коэффициентом. Обычно предполагается, что случайная величина εi имеет нормальный закон распределения с математическим ожиданием равным нулю и с дисперсией σ2.
Анализ уравнения (4.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (4.2):
Y = X α + ε (4.2)
где Y — вектор зависимой переменной размерности n×1, представляющий собой n наблюдений значений yj,
X — матрица n наблюдений независимых переменных Х1, Х2, Х3, ..., Хm, размерность матрицы X равна n×(m+1);
α — подлежащий оцениванию вектор неизвестных параметров размерности (m+1) ×1;
ε — вектор случайных отклонений (возмущений) размерности n×1.
Таким образом,
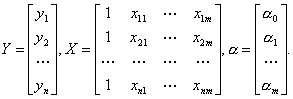
Уравнение (4.1) содержит значения неизвестных параметров α0, α1, α2, ..., αm. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрессии, в которой вместо истинных значений параметров подставлены их оценки (а именно такие регрессии и применяются на практике), имеет вид:
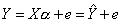 , (4.3)
, (4.3)
где α — вектор оценок параметров;
е — вектор «оцененных» отклонений регрессии, остатки регрессии ε = Y - X α;
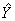 — оценка значений Y,
равная Ха.
— оценка значений Y,
равная Ха.
Оценка параметров модели множественной регрессии с помощью метода наименьших квадратов.
Формулу для вычисления параметров регрессионного уравнения приведем без вывода:
а = (ХТХ)-1XTY. (4.4)
Одним из условий регрессионной модели является предположение о линейной независимости объясняющих переменных, т.е., решение задачи возможно лишь тогда, когда столбцы и строки матрицы исходных данных линейно независимы. Для экономических показателей это условие выполняется не всегда. Линейная или близкая к ней связь между факторами называется мультиколлинеарностью и приводит к линейной зависимости нормальных уравнений, что делает вычисление параметров либо невозможным, либо затрудняет содержательную интерпретацию параметров модели. Мультиколлинеарность может возникать в силу разных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания. В частности, так может случиться, когда значения одной независимой переменной являются датированными значениями другой. Считают явление мультиколлинеарности в и сходных данных установленным, если коэффициент парной корреляции между двумя переменными больше 0,8. Чтобы избавиться от мультиколлинеарности, в модель включают лишь один из линейно связанных между собой факторов, причем тот, который в большей степени связан с зависимой переменной.
В качестве критерия мультиколлинеарности может быть принято соблюдение следующих неравенств:
ryxi > rxixk, ryxk > rxixk, rxixk < 0,8.
Если приведенные неравенства (или хотя бы одно из них) не выполняются, то в модель включают тот фактор, который наиболее тесно связан с Y.
Анализ статистической значимости параметров модели. Значимость отдельных коэффициентов регрессии проверяется по t-статистике путем проверки гипотезы о равенстве нулю j-го параметра уравнения (кроме свободного члена):
Taj = aj/Saj, (4.5)
где Saj — стандартное (среднеквадратическое) отклонение коэффициента уравнения регрессии aj.
Величина Saj представляет собой квадратный
корень из произведения несмещенной оценки дисперсии
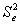 и j-го диагонального элемента
матрицы, обратной матрице системы нормальных уравнений.
и j-го диагонального элемента
матрицы, обратной матрице системы нормальных уравнений.
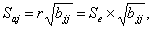 (4.6)
(4.6)
где bjj — диагональный элемент матрицы (ХТХ)-1.
Если расчетное значение t-критерия с (n-k-1) степенями свободы превосходит его табличное значение при заданном уровне значимости, коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, следует исключить из модели (при этом ее качество не ухудшится).
Проверка значимости модели регрессии. Для проверки значимости модели регрессии используется F-критерий Фишера, вычисляемый по формуле (3.14).
Оценка качества модели регрессии
Качество модели оценивается стандартным для математических моделей образом: по адекватности и точности на основе анализа остатков регрессии е. Расчетные значения получаются путем подстановки в модель фактических значений всех включенных факторов.
Анализ остатков позволяет получить представление, насколько хорошо подобрана сама модель и насколько правильно выбран метод оценки коэффициентов. Согласно общим предположениям регрессионного анализа остатки должны вести себя как независимые (в действительности почти независимые) одинаково распределенные случайные величины. В классических методах регрессионного анализа предполагается также нормальный закон распределения остатков.
Независимость остатков проверяется с помощью критерия Дарбина-Уотсона.
Исследование остатков полезно начинать с изучения их графика. Он может показать наличие какой-то зависимости, не учтенной в модели. Скажем, при подборе простой линейной зависимости между Y и X график остатков может показать необходимость перехода к нелинейной модели (квадратичной, полиномиальной, экспоненциальной) или включения в модель периодических компонент.
Выбросы. График остатков хорошо показывает и резко отклоняющиеся от модели наблюдения — выбросы. Подобным аномальным наблюдениям надо уделять особо пристальное внимание, так как их присутствие может грубо искажать значения оценок. Устранение эффектов выбросов может проводиться либо с помощью удаления этих точек из, анализируемых данных (эта процедура называется цензурированием), либо с помощью применения методов оценивания параметров, устойчивых к подобным грубым отклонениям.
Для оценки качества модели множественной регрессии вычисляют коэффициент множественной корреляции (индекс корреляции) R и коэффициент детерминации R2 (см. формулы 3.9 и 3.13).
В многофакторной регрессии добавление дополнительных объясняющих
переменных увеличивает коэффициент детерминации. Следовательно, коэффициент
детерминации должен быть скорректирован с учетом числа независимых переменных.
Скорректированный R2, или
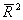 , рассчитывается так:
, рассчитывается так:
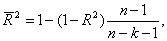
где n — число наблюдений;
k — число независимых переменных.
Оценка влияния отдельных факторов на зависимую переменную на основе модели (коэффициенты эластичности, β-коэффициенты).
Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Однако непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени колеблемости. Для устранения таких различий при интерпретации применяются средние частные коэффициенты эластичности Э(j) и бета-коэффициенты β(j), которые рассчитываются соответственно по формулам:
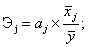 (4.7)
(4.7)
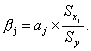 (4.8)
(4.8)
где Sxj — среднеквадратическое отклонение фактора j.
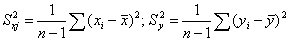 .
.
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора. j на один процент. Однако он не учитывает степень колеблемости факторов.
Бета-коэффициент показывает, на какую часть величины среднего квадратического отклонения Sy изменится зависимая переменная Y с изменением соответствующей независимой переменной Xj на величину своего среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных.
Указанные коэффициенты позволяют упорядочить факторы по степени влияния факторов на зависимую переменную.
Долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов D(j):
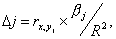
где 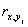 — коэффициент парной
корреляции между фактором j (j = 1, ..., m) и зависимой
переменной.
— коэффициент парной
корреляции между фактором j (j = 1, ..., m) и зависимой
переменной.
Использование многофакторных моделей для анализа и прогнозирования развития экономических систем. Одна из важнейших целей моделирования заключается в прогнозировании поведения исследуемого объекта. Обычно термин «прогнозирование» используется в тех ситуациях, когда требуется предсказать состояние системы в будущем. Для регрессионных моделей он имеет, однако, более широкое значение. Как уже отмечалось, данные могут не иметь временной структуры, но и в этих случаях вполне может возникнуть задача оценки значения зависимой переменной для некоторого набора независимых, объясняющих переменных, которых нет в исходных наблюдениях. Именно в этом смысле — как построение оценки зависимой переменной — и следует понимать прогнозирование в эконометрике.
При использовании построенной модели для прогнозирования делается предположение о сохранении в период прогнозирования существовавших ранее взаимосвязей переменных.
Для прогнозирования зависимой переменной на l шагов вперед необходимо знать прогнозные значения всех входящих в нее факторов. Их оценки могут быть получены на основе временных экстраполяционных моделей или заданы пользователем. Эти оценки подставляются в модель и получаются прогнозные оценки.
Построение точечных и интервальных прогнозов на основе регрессионной модели. Какие факторы влияют на ширину доверительного интервала?
Для того чтобы определить область возможных значений результативного показателя, при рассчитанных значениях факторов следует учитывать два возможных источника ошибок: рассеивание наблюдений относительно линии регрессии и ошибки, обусловленные математическим аппаратом построения самой линии регрессии. Ошибки первого рода измеряются с помощью характеристик точности, в частности величиной Sy. Ошибки второго рода обусловлены фиксацией численного значения коэффициентов регрессии, в то время как они в действительности являются случайными, нормально распределенными.
Для линейной модели регрессии доверительный интервал рассчитывается следующим образом. Оценивается величина отклонения от линии регрессии (обозначим ее U):
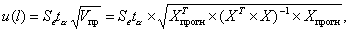 (4.9)
(4.9)
где 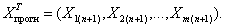
Пример 4.1. Задача состоит в построении модели для предсказания объема реализации одного из продуктов фирмы.
Объем реализации - это зависимая переменная Y (млн. руб.) В качестве независимых, объясняющих переменных выбраны: время – Х1, расходы на рекламу Х2 (тыс. руб.), цена товара Х3 (руб.), средняя цена товара у конкурентов X4 (pyб.), индекс потребительских расходов Х5 (%).
Требуется:
1. Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.
2. Рассчитать параметры модели.
3. Для оценки качества модели определить:
• линейный коэффициент множественной корреляции,
• коэффициент детерминации.
4. Осуществить оценку значимости уравнения регрессии.
5. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
6. Оценить влияние факторов на зависимую переменную по модели.
7. Построить точечный и интервальный прогноз результирующего показателя.
1. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции. Выбор факторных признаков для построения двухфакторной регрессионной модели.
Статистические данные по всем переменным приведены в таблице 4.1. В этом примере n = 16, m = 5.
Таблица 4.1
| Y | X1 | Х2 | Х3 | Х4 | X5 |
|---|---|---|---|---|---|
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов |
| 126 | 1 | 4,0 | 15,0 | 17,0 | 100,0 |
| 137 | 2 | 4,8 | 14,8 | 17,3 | 98,4 |
| 148 | 3 | 3,8 | 15,2 | 16,8 | 101,2 |
| 191 | 4 | 8,7 | 15,5 | 16,2 | 103,5 |
| 274 | 5 | 8,2 | 15,5 | 16,0 | 104,1 |
| 370 | 6 | 9,7 | 16,0 | 18,0 | 107,0 |
| 432 | 7 | 14,7 | 18,1 | 20,2 | 107,4 |
| 445 | 8 | 18,7 | 13,0 | 15,8 | 108,5 |
| 367 | 9 | 19,8 | 15,8 | 18,2 | 108,3 |
| 367 | 10 | 10,6 | 16,9 | 16,8 | 109,2 |
| 321 | 11 | 8,6 | 16,3 | 17,0 | 110,1 |
| 307 | 12 | 6,5 | 16,1 | 18,3 | 110,7 |
| 331 | 13 | 12,6 | 15,4 | 16,4 | 110,3 |
| 345 | 14 | 6,5 | 15,7 | 16,2 | 111,8 |
| 364 | 15 | 5,8 | 16,0 | 17,7 | 112,3 |
| 384 | 16 | 5,7 | 15,1 | 16,2 | 112,9 |
В таблице 4.2. приведены промежуточные результаты при вычислении коэффициента корреляции по формуле (3.1)
Таблица 4.2
| t | Y | Х2 | 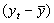 |
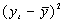 |
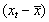 |
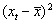 |
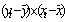 |
|---|---|---|---|---|---|---|---|
| 1 | 126 | 4,0 | -180,813 | 32693,16 | -5,29375 | 28,02379 | 957,1762 |
| 2 | 137 | 4,8 | -169,813 | 28836,29 | -4,49375 | 20,19379 | 763,0949 |
| 3 | 148 | 3,8 | -158,813 | 25221,41 | -5,49375 | 30,18129 | 872,4762 |
| 4 | 191 | 8,7 | -115,813 | 13412,54 | -0,59375 | 0,352539 | 68,76367 |
| 5 | 274 | 8,2 | -32,8125 | 1076,66 | -1,09375 | 1,196289 | 35,88867 |
| 6 | 370 | 9,7 | 63,1875 | 3992,66 | 0,40625 | 0,165039 | 25,66992 |
| 7 | 432 | 14,7 | 125,1875 | 15671,91 | 5,40625 | 29,22754 | 676,7949 |
| 8 | 445 | 18,7 | 138,1875 | 19095,79 | 9,40625 | 88,47754 | 1299,826 |
| 9 | 367 | 19,8 | 60,1875 | 3622,535 | 10,50625 | 110,3813 | 632,3449 |
| 10 | 367 | 10,6 | 60,1875 | 3622,535 | 1,30625 | 1 ,706289 | 78,61992 |
| 11 | 321 | 8,6 | 14,1875 | 201 ,2852 | -0,69375 | 0,481289 | -9,84258 |
| 12 | 307 | 6,5 | 0,1875 | 0,035156 | -2,79375 | 7,805039 | -0,52383 |
| 13 | 331 | 12,6 | 24,1875 | 585,0352 | 3,30625 | 10,93129 | 79,96992 |
| 14 | 345 | 6,5 | 38,1875 | 1458,285 | -2,79375 | 7,805039 | -106,686 |
| 15 | 364 | 5,8 | 57,1875 | 3270,41 | -3,49375 | 12,20629 | -199,799 |
| 16 | 384 | 5,7 | 77,1875 | 5957,91 | -3,59375 | 12,91504 | -277,393 |
| Сумма | 4909 | 148,7 | 0 | 158718,4 | 0 | 362,0494 | 4696,381 |
| Среднее значение | 306,8125 | 9,29375 | 0 |
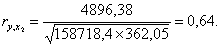
Использование инструмента Корреляция (Анализ данных в EXCEL).
Для проведения корреляционного анализа выполните следующие действия:
1. Данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек.
2. Выберите команду Сервис => Анализ данных.
3. В диалоговом окне Анализ данных выберите инструмент Корреляция, а затем щелкните на кнопке ОК.
4. В диалоговом окне Корреляция в поле Входной интервал необходимо ввести диапазон ячеек, содержащих исходные данные. Если выделены и заголовки столбцов, то установите флажок Метки в первой строке.
5. Выберите параметры вывода. В данном примере Новый рабочий лист.
6. ОК.
Таблица 4.3
Результат корреляционного анализа
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов | |
|---|---|---|---|---|---|---|
| Столбец 1 | Столбец 2 | Столбец 3 | Столбец 4 | Столбец 5 | Столбец 6 | |
| Объем реализации | 1 | |||||
| Время | 0,678 | 1 | ||||
| Реклама | 0,646 | 0106 | 1 | |||
| Цена | 0,233 | 0,174 | -0,003 | 1 | ||
| Цена конкурента | 0,226 | -0,051 | 0,204 | 0,698 | 1 | |
| Индекс потребительских расходов | 0,816 | 0,960 | 0,273 | 0,235 | 0,03 | 1 |
Анализ матрицы коэффициентов парной корреляции показывает, что зависимая переменная, т.е. объем реализации имеет тесную связь с индексом потребительских расходов (rух5 = 0,816), с расходами на рекламу (rух2 = 0,646) и со временем (rух1 = 0,678). Однако факторы Х2 и Х5 тесно связаны между собой (rx1x5 = 0,96), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели Х5 — индекс потребительских расходов. В этом примере n = 16, m = 5, после исключения незначимых факторов n = 16, k = 2.
2. Выбор вида модели и оценка ее параметров
Оценка параметров регрессии осуществляется по методу наименьших квадратов по формуле (4.4), используя данные, приведенные в таблице 4.411.
Таблица 4.4
| Y | Х0 | X1 | Х2 |
|---|---|---|---|
| Объем реализации | Реклама | Индекс потребительских расходов | |
| 126 | 1 | 4,0 | 100 |
| 137 | 1 | 4,8 | 98,4 |
| 148 | 1 | 3,8 | 101,2 |
| 191 | 1 | 8,7 | 103,5 |
| 274 | 1 | 8,2 | 104,1 |
| 370 | 1 | 9,7 | 107,0 |
| 432 | 1 | 14,7 | 107,4 |
| 445 | 1 | 18,7 | 108,5 |
| 367 | 1 | 19,8 | 108,3 |
| 367 | 1 | 10,6 | 109,2 |
| 321 | 1 | 8,6 | 110,1 |
| 307 | 1 | 6,5 | 110,7 |
| 331 | 1 | 12,6 | 110,3 |
| 345 | 1 | 6,5 | 111,8 |
| 364 | 1 | 5,8 | 112,3 |
| 384 | 1 | 5,7 | 112,9 |
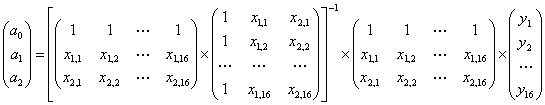

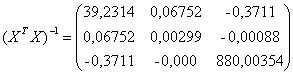
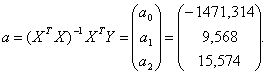
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
у = -1471,314 + 9,568x1, + 15,754x2
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого наблюдения.
Применение инструмента Регрессия (Анализ данных в EXCEL).
Для проведения регрессионного анализа выполните следующие действия:
1. Выберите команду Сервис => Анализ данных.
2. В диалоговом окне Анализ данных выберите инструмент Регрессия, а затем щелкните на кнопке ОК.
3. В диалоговом окне Регрессия в поле Входной интервал Y введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле Входной интервал X введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных (рис. 4.1).
4. Если выделены и заголовки столбцов, то установите флажок Метки в первой строке.
5. Выберите параметры вывода. В данном примере Новая рабочая книга.
6. В поле Остатки поставьте необходимые флажки.
7. ОК.
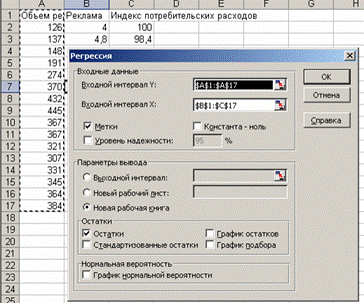
Рис. 4.1. Диалоговое окно Регрессия подготовлено к выполнению анализа данных
Результат регрессионного анализа содержится в таблицах 4.5-4.8. Рассмотрим содержание этих таблиц.
Таблица 4.5
| Регрессионная статистика | |
|---|---|
| Множественный R | 0,927 |
| R-квадрат | 0,859 |
| Нормированный R-квадрат | 0,837 |
| Стандартная ошибка | 41,473 |
| Наблюдения | 16,000 |
Таблица 4.6
| Дисперсионный анализ | ||||
|---|---|---|---|---|
| df | SS | MS | F | |
| Регрессия | 2 | 136358,334 | 68179,167 | 39,639 |
| Остаток | 13 | 22360,104 | 1720,008 | |
| Итого | 15 | 158718,438 | ||
Таблица 4.7
| Коэффициенты | Стандартная ошибка | t-статистика | |
|---|---|---|---|
| Y-пересечение | -1471,31 | 259,766 | -5,664 |
| Реклама | 9,568 | 2,266 | 4,223 |
| Индекс потребительских расходов | 15,753 | 2,467 | 6,386 |
Таблица 4.8
| Вывод остатка | ||
|---|---|---|
| Наблюдение | Предсказанное | Остатки |
| 1 | 142,25 | -16,25 |
| 2 | 124,70 | 12,30 |
| 3 | 159,24 | -11,24 |
| 4 | 242,35 | -51,35 |
| 5 | 247,02 | 26,98 |
| 6 | 307,06 | 62,94 |
| 7 | 361,20 | 70,80 |
| 8 | 416,80 | 28,20 |
| 9 | 424,18 | -57,18 |
| 10 | 350,32 | 16,68 |
| 11 | 345,37 | -24,37 |
| 12 | 334,72 | -27,72 |
| 13 | 386,79 | -55,79 |
| 14 | 352,05 | -7,05 |
| 15 | 353,23 | 10,77 |
| 16 | 361,73 | 22,27 |
Пояснения к таблице 4.5
Регрессионная статистика
| № | Наименование в отчете EXCEL | Принятые наименования | Формула |
|---|---|---|---|
| 1 | Множественный R | Коэффициент множественной корреляции, индекс корреляции | 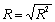 |
| 2 | R-квадрат | Коэффициент детерминации, R2 | 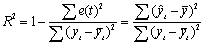 |
| 3 | Нормированный R-квадрат | Скорректированный R2 | 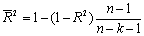 |
| 4 | Стандартная ошибка | Стандартная ошибка оценки | 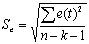 |
| 5 | Наблюдения | Количество наблюдений, n | n |
Пояснения к таблице 4.6
| Df - число степеней свободы | SS - сумма квадратов | MS | F-критерий Фишера | |
|---|---|---|---|---|
| Регрессия | k=2 | 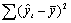 |
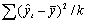 |
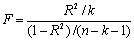 |
| Остаток | n-k-1 = 13 | 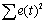 |
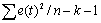 |
|
| Итого | n-1 = 15 | 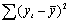 |
Пояснения к таблице 4.7.
Во втором столбце таблицы 4.7 содержатся коэффициенты уравнения регрессии а0, а1, а2. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии (4.6), а в четвертом - t-статистика (4.5), используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
У = -1471,314 + 9,568х1 + 15,754х2.
3. Оценка качества модели
В таблице 4.8 приведены вычисленные по модели значения Y и значения остаточной компоненты.
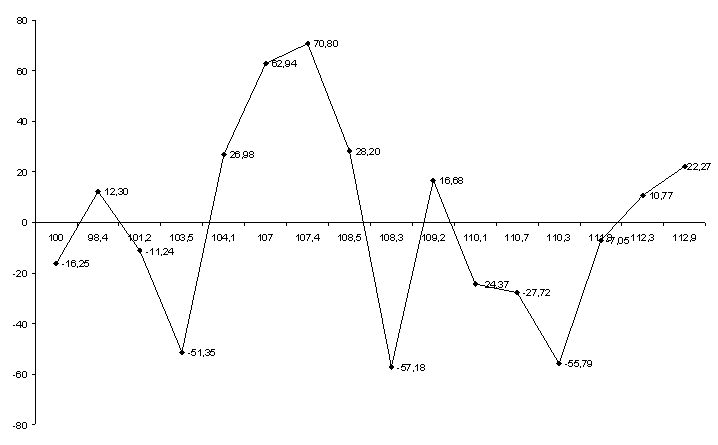
Рис. 4.1. График остатков
Проверку независимости проведем с помощью d-критерия Дарбина-Уотсона.
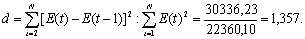
В качестве критических табличных уровней при N=16, двух объясняющих факторах при уровне значимости в 5% возьмем величины d1=0,98 и d2=1,54.
Так как расчетное значение попало в интервал от d1 до d2, то нельзя сделать окончательный вывод по этому критерию. Для определения степени автокорреляции вычислим коэффициент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки.
Стандартная ошибка коэффициента корреляции рассчитывается следующим образом:
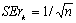 .
.
Коэффициенты автокорреляции случайных данных обладают выборочным
распределением, приближающимся к нормальному с нулевым математическим ожиданием
и средним квадратическим отклонением, равным
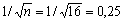 .
.
Если r1 находится в интервале 1,96 × 0,25 ≤ r1 × 1,96 ≤ 0,25, то можно считать, что данные не показывают наличие автокорреляции первого порядка, т.к. -0,49 ≤ r1 = 0,309 ≤ 0,49, и свойство независимости выполняется.
Вычислим для модели коэффициент детерминации.
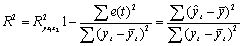
R2 = 1-22360,104/158718,44 = 136358,3/158718,44 = 0,859.
Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов. Значение коэффициента детерминации можно найти в таблице 4.5.
Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:
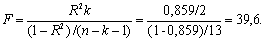
Значение F-критерия Фишера можно найти в таблице 4.6 протокола EXCEL.
Табличное значение F -критерия при доверительной вероятности 0,95 при V1 = k =2 и V1 = n-k-1 = 16-2-1 = 13 составляет 3,81. Табличное значение F-критерия можно найти с помощью функции FРАСПОБР (рис. 4.2).
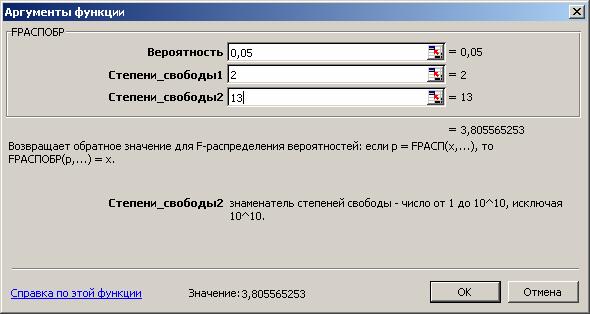
Рис. 4.2. Определение табличного значения F-критерия
Поскольку Fpac > Fтабл, уравнение регрессии следует признать адекватным.
4. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
Значимость коэффициентов уравнения регрессии а0, а1, а2 оценим с использованием t-критерия Стьюдента.
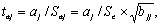

b11 = 39,2314
b22 = 0,00299
b33 = 0,00354
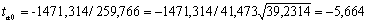
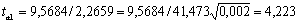
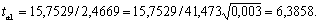
Расчетные значения t-критерия Стьюдента для коэффициентов уравнения регрессии а1, а2 приведены в четвертом столбце таблицы 4.7 протокола EXCEL. Табличное значение t-критерия Стьюдента можно найти с помощью функции СТЬЮДРАСПОБР (рис. 4.3) .
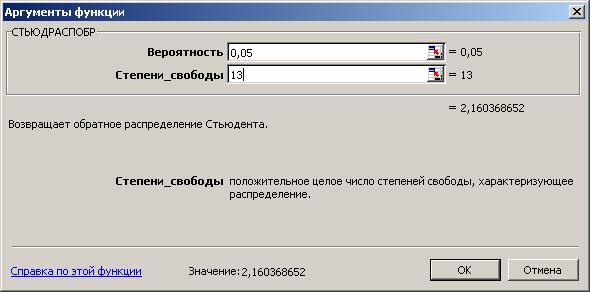
Рис. 4.3. Определение табличного значения t-критерия Стьюдента
Табличное значение t-критерия при 5% уровне значимости и степенях свободы (16-2-1 = 13) составляет 2,16. Так как |tрас|> tтабл, то коэффициенты а1, а2 и существенны (значимы).
5. Проанализировать влияние факторов на зависимую переменную по модели (для каждого коэффициента регрессии вычислить коэффициент эластичности, β-коэффициент).
Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент эластичности (Э) и бета-коэффициент, которые соответственно рассчитываются по формулам:
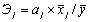
Э1 = 9,568 × 9,294/306,813 = 0,2898
Э1 = 15,7529 × 107,231/306,813 = 5,506
βi = αi × Sxi : Sy
βi = 9,568 × 4,913/102,865 = 0,457
βi = 15,7529 × 4,5128/102,865 = 0,691.
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на один процент.
Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных. Это означает, что при увеличении затрат на рекламу в нашем примере на 4,91 тыс. руб. объем реализации увеличится на 47 тыс. руб. (0,457 × 102,865).
6. Определить точечные и интервальные прогнозные оценки объема реализации на два квартала вперед (t0,7 = 1,12).
Прогнозные значения Х1,17, Х2,17 и Х1,18, Х1,18 можно определить с помощью методов экспертных оценок, с помощью средних абсолютных приростов или вычислить на основе экстраполяционных методов.
Для фактора Х1 Затраты на рекламу выбрана модель
Х1 = 12,83 - 11,616t + 4,319t2 - 0,552t3 + 0,020t4 - 0,0006t5,
по которой получен прогноз на 2 месяца вперед2. График модели временного ряда Затраты на рекламу приведен на рис. 4.4.
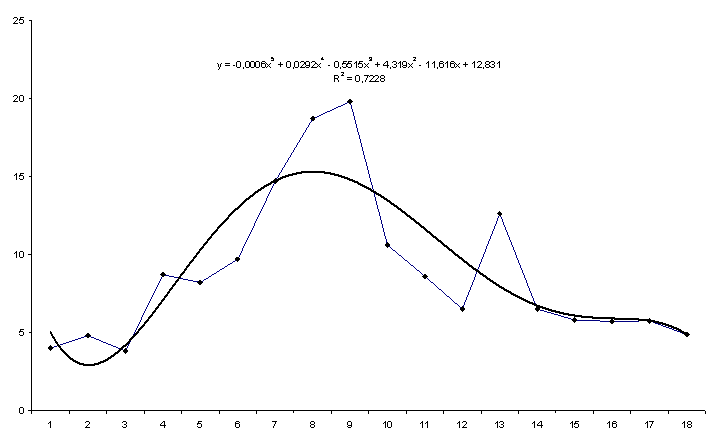
Рис. 4.4. Прогноз показателя Затраты на рекламу
| Упреждение - 1 | Упреждение - 2 |
| Прогноз — 5,75 | Прогноз - 4,85 |
Для временного ряда Индекс потребительских расходов в качестве аппроксимирующей функции выбран полином второй степени (парабола), но которой построен прогноз на 2 шага вперед. На рисунке 4.5 приведен результат построения тренда для временного ряда Индекс потребительских расходов.
Х2 = 97,008 + 1,739 t - 0,0488 t2.
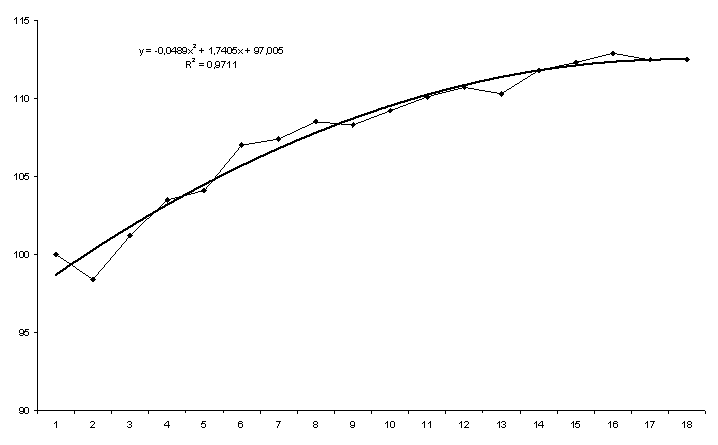
Рис. 4.5. Прогноз показателя Индекс потребительских расходов
| Упреждение - 1 | Упреждение - 2 |
| Прогноз — 112,468 | Прогноз - 112,488 |
Для получения прогнозных оценок зависимостей переменной по модели Y = -1471,438 + 9,568Х1 + 15,754 Х2
подставим в нее найденные прогнозные значения факторов Х1 и Х2
Yt=17 = -1471,438 + 9,568 × 5,75 + 15,754 × 112,468 = 355,399
Yt=18 = -1471,438 + 9,568 × 4,85 +15,754 × 112,488 = 344,179.
Доверительный интервал прогноза будет иметь следующие границы:
Верхняя граница прогноза: Yp(N+1) + U(1)
Нижняя граница прогноза: Yp(N+1) - U(1).
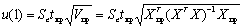
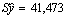
tкр = 2.163
1=1
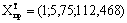
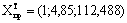
u(1) = 42,968
1=2
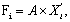
u(2) = 45,749.
Результаты прогнозных оценок модели регрессии представим в табл. 4.2.5.
Таблица 4.2.5
Таблица прогнозов (р = 95%)
| Упреждение | Прогноз | Нижняя граница | Верхняя граница |
|---|---|---|---|
| 1 | 355,399 | 312,368 | 398,367 |
| 2 | 344,179 | 298,43 | 389,928 |
1 Для вычисления а0 добавлен столбец Х0.
2 Внимание! Полиномы таких высоких порядков редко используются при прогнозировании экономических показателей.
3 Значение tкр получено с помощью функции СТЬЮДРАСПРОБР(0,05;13) для выбранной вероятности 95% с числом степеней свободы равным 13.