Тема 1. Введение. Эконометрика и эконометрическое моделирование
Тема 3. Парная регрессия и корреляция
Тема 4. Модель множественной регрессии
Тема 5. Системы линейных одновременных уравнений
Тема 6. Многомерный статистический анализ
Задание для выполнения контрольной работы по дисциплине «Эконометрика»
Задание для выполнения лабораторной работы. Задачи для ЭВМ (СТАТЭКСПЕРТ)
Тема 6. Многомерный статистический анализ
Данная тема знакомит студентов с некоторыми методами многомерного статистического анализа (МСА), которые получили наибольшее распространение. При изучении данной темы необходимо уделить особое внимание типам задач, для решения которых используются методы МСА. Технология решения задач подробно рассмотрена в [7]. Практическое применение методов МСА требует обязательного использования вычислительной техники и специального программного обеспечения. Программа курса предусматривает по данной теме выполнение лабораторной работы с помощью программы СтатЭксперт.
Факторный и компонентный анализ в большинстве случаев проводятся совместно.
Компонентный анализ является методом определения структурной зависимости между случайными переменными. В результате его использования получается сжатое описание малого объема, несущее почти всю информацию, содержащуюся в исходных данных. Главные компоненты получаются из исходных переменных путем целенаправленного вращения, т.е. как линейные комбинации исходных переменных. Вращение производится таким образом, чтобы главные компоненты были ортогональны и имели максимальную дисперсию среди возможных линейных комбинаций исходных переменных X. При этом переменные не коррелированы между собой и упорядочены по убыванию дисперсии (первая компонента имеет наибольшую дисперсию). Кроме того, общая дисперсия после преобразования остается без изменений.
Факторный анализ является более общим методом преобразования исходных переменных по сравнению с компонентным анализом.
Факторный анализ. Центральной проблемой, которую приходится решать при обработке экспериментальных данных, представленных в виде матрицы, является задача ее «сжатия», выделения «существенной» информации, которая затемнена и искажена разного рода данными, не имеющими отношения к сути изучаемого явления. Получаемые в исследованиях матрицы данных часто содержат десятки параметров и сотни объектов (систем). Поэтому стремление «сжать» информацию, содержащуюся в этой матрице, преследует цель сделать данные обозримыми. И еще одна цель такого «сжатия». Так как большой массив данных удалось представить в виде малого массива, то это дает основание надеяться, что выявлена некоторая закономерность изучаемого явления; и чем сильнее удалось «сжать» исходную информацию, тем больше оснований для такой надежды.
Одним из наиболее эффективных средств «сжатия» информации, содержащейся в матрице исходных данных, является комплекс моделей и методов, называемых факторным анализом. Кроме того, факторный анализ — это метод формирования гипотез, так как эффективно показывает скрытые закономерности данного объекта (системы, процесса).
Действительно, наблюдаемые или изменяемые параметры являются лишь косвенными характеристиками изучаемого объекта. На самом же деле существуют внутренние (скрытые, не наблюдаемые непосредственно) параметры или свойства, число которых мало и которые определяют значения наблюдаемых параметров. Эти внутренние параметры принято называть факторами. Задача факторного анализа — представить наблюдаемые параметры в виде линейных комбинации факторов и, может быть, некоторых дополнительных «несущественных» величин — помех.
Кластерный анализ — это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое из которых описывается набором признаков (параметров) Х1, Х2, ..., Хk. Целью кластерного анализа является образование групп схожих между собой объектов, которые принято называть кластерами (класс, таксон, сгущение).
Кластерный анализ — одно из направлений статистического исследования. Особо важное место он занимает в тех отраслях науки, которые связаны с изучением массовых явлений и процессов. Необходимость развития методов кластерного анализа и их использования продиктована тем, что они помогают построить научно обоснованные классификации, выявить внутренние связи между единицами наблюдаемой совокупности. Кроме того, методы кластерного анализа могут использоваться в целях сжатия информации, что является важным фактором в условиях постоянного увеличения и усложнения потоков статистических данных.
Методы кластерного анализа позволяют решать следующие задачи [2]:
• проведение классификации объектов с учетом признаков, отражающих сущность, природу объектов. Решение такой задачи, как правило, приводит к углублению знаний о совокупности классифицируемых объектов;
• проверка выдвигаемых предположений о наличии некоторой структуры в изучаемой совокупности объектов, т.е. поиск существующей структуры;
• построение новых классификаций для слабоизученных явлений, когда необходимо установить наличие связей внутри совокупности и попытаться привнести в нее структуру.
Дискриминантный анализ является разделом многомерного статистического анализа, который включает в себя методы классификации многомерных наблюдений по принципу максимального сходства при наличии обучающих признаков.
Напомним, что в кластерном анализе рассматриваются методы многомерной классификации без обучения. В дискриминантном анализе новые кластеры не образуются, а формулируется правило, по которому объекты подмножества подлежащего классификации относятся к одному из уже существующих (обучающих) подмножеств (классов), на основе сравнения величины дискриминантной функции классифицируемого объекта, рассчитанной по дискриминантным переменным, с некоторой константой дискриминации.
Предположим, что существуют две или более совокупности (группы) и что мы располагаем множеством выборочных наблюдений над ними. Основная задача дискриминантного анализа состоит в построении с помощью этих выборочных наблюдений правила, позволяющего отнести новое наблюдение к одной из совокупностей.
Постановка задачи дискриминантного анализа. Пусть имеется множество М единиц N объектов наблюдения, каждая i-я единица которого описывается совокупностью р значений дискриминантных переменных (признаков) xij, (i = 1, 2, ..., N; j = 1, 2, ..., р). Причем все множество М объектов включает q обучающих подмножеств (q ≥ 2) Mk размером nk каждое и подмножество М0 объектов подлежащих дискриминации (под дискриминацией понимается различие). Здесь k — номер подмножества (класса), k = 1, 2, ..., q.
Требуется установить правило (линейную или нелинейную дискриминантную функцию f(X)) распределения m-объектов подмножества М0 по подмножествам Mk.
Наиболее часто используется линейная форма дискриминантной функции, которая представляется в виде скалярного произведения векторов A = (a1, a2, ..., ap) дискриминантных множителей и вектора Xi = (xi,1, xi,2, …, xi,p) дискриминантных переменных:
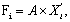 (6.1)
(6.1)
или Fi = a1 xi,1 + a2 xi,2 + … ap xi,p
Здесь Xi — транспонированный вектор дискриминантных переменных xij — значений j-х признаков у i-го объекта наблюдения.
Дискриминантный анализ проводится в условиях следующих основных предположений:
— множество М объектов разбито на два или более (q≥2) подмножеств Mk (класса), которые отличаются от других групп переменными xij;
— в каждом подмножестве Mk находится, по крайней мере, два объекта (nk≥2), причем все объекты наблюдения множества М должны принадлежать какому-либо из подмножеств (классов);
— число N объектов наблюдения должно превышать число р дискриминантных переменных (0<р<N-2) не менее чем на две единицы;
— линейная независимость между признаками (j), т.е. ни один из признаков не должен быть линейной комбинацией других признаков, в противном случае он не несет новой информации;
— нормальный закон распределения дискриминантных переменных xij (по признакам).
Если приведенные предположения не удовлетворяются, то ставится вопрос о целесообразности использования дискриминантного анализа для классификации новых наблюдений.
Основными проблемами дискриминантного анализа являются отбор дискриминантных переменных и выбор вида дискриминантной функции. Для получения наилучших различий обучающих подмножеств могут использоваться критерии последовательного отбора переменных [6] или пошаговый дискриминантный анализ. После определения набора дискриминантных переменных решается вопрос о выборе вида дискриминантной функции (линейной или нелинейной).
В качестве дискриминантных переменных могут выступать не только исходные (наблюдаемые) признаки, но и главные компоненты или главные факторы, выделенные в факторном анализе.
Дискриминантный анализ может использоваться и для прогнозирования поведения наблюдаемых единиц статистической совокупности путем сопоставления их с поведением аналогичных объектов обучающих подмножеств.
Алгоритм выполнения дискриминантного анализа рассмотрен применительно к линейной дискриминантной функции вида (6.1). Его основные этапы.
1. Исходные данные представляются либо в табличной форме в виде q подмножеств (обучающих выборок) Mk и подмножества М0 объектов подлежащих дискриминации, либо сразу в виде матриц X(1), X(2), ..., X(q), размером (nk×p):
| Номер подмножества Mk (k = 1, 2, ..., q) | Номер объекта, i (i = 1, 2, ..., nk1) | Свойства (показатель), j (j = 1, 2, ..., p) | |||
|---|---|---|---|---|---|
| х1 | х2 | … | х0 | ||
| Подмножество M1 (k = 1) | 1 | 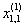 |
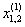 |
… | 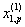 |
| 2 | 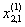 |
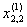 |
… | 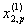 |
|
| … | … | … | … | … | |
| n1 | 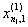 |
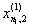 |
… | 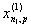 |
|
| Подмножество M2 (k = 2) | 1 | 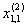 |
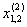 |
… | 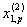 |
| 2 | 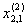 |
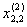 |
… | 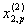 |
|
| … | … | … | … | … | |
| n2 | 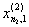 |
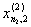 |
… | 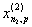 |
|
| … | … | … | … | … | … |
| Подмножество Mq (k = q) | 1 | 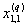 |
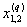 |
… | 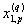 |
| 2 | 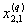 |
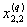 |
… | 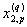 |
|
| … | … | … | … | … | |
| nq | 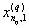 |
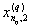 |
… | 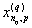 |
|
| Подмножество M0, подлежащее дискриминации | 1 | 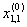 |
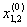 |
… | 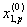 |
| 2 | 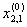 |
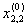 |
… | 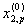 |
|
| … | … | … | … | … | |
| m | 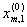 |
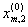 |
… | 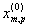 |
|
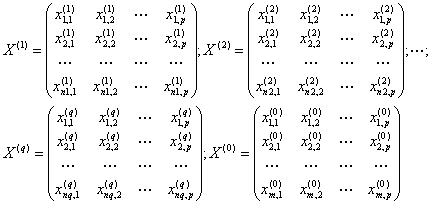
где X(k) - матрицы с обучающими признаками (k = 1, 2, ..., q),
X(0) матрица новых m-объектов, подлежащих дискриминации (размером m×p), р — количество свойств, которыми характеризуется каждый i-й объект.
Здесь должно выполняться условие: общее количество объектов
N множества М должно быть равно сумме количества объектов
m (в подмножестве M0), подлежащих дискриминации,
и общего количества объектов 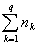 в обучающих
подмножествах:
в обучающих
подмножествах: 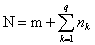 , где q - количество
обучающих подмножеств (q≥2). В реальной практике наиболее часто реализуется
случай q=2, поэтому и алгоритм дискриминантного анализа приведен
для данного варианта.
, где q - количество
обучающих подмножеств (q≥2). В реальной практике наиболее часто реализуется
случай q=2, поэтому и алгоритм дискриминантного анализа приведен
для данного варианта.
2. Определяются 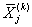 элементы
векторов
элементы
векторов 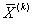 средних значений по каждому
j-му признаку для i объектов внутри k-го подмножества
(k = 1, 2):
средних значений по каждому
j-му признаку для i объектов внутри k-го подмножества
(k = 1, 2):
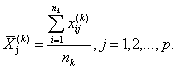
Результаты расчета представляются в виде векторов столбцов
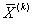 :
:
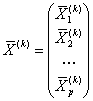
3. Для каждого обучающего подмножества рассчитываются ковариационные матрицы S(k) (размером p×p):
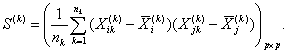
4. Рассчитывается объединенная ковариационная матрица
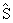 по формуле:
по формуле:
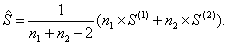
5. Рассчитывается матрица 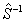 обратная к объединенной ковариационной матрице
обратная к объединенной ковариационной матрице
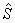 :
:
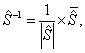
где 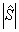 — определитель матрицы
— определитель матрицы
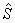 , (причем
, (причем
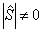 ),
),
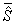 — присоединенная матрица,
элементы которой являются алгебраическими дополнениями элементов матрицы
— присоединенная матрица,
элементы которой являются алгебраическими дополнениями элементов матрицы
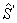 .
.
6. Рассчитывается вектор-столбец
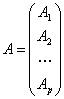 дискриминантных множителей с учетом всех
элементов обучающих подмножеств по формуле:
дискриминантных множителей с учетом всех
элементов обучающих подмножеств по формуле:
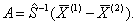
Данная расчетная формула получена с помощью метода наименьших квадратов из условия обеспечения наибольшего различия между дискриминантными функциями. Наилучшее разделение двух обучающих подмножеств обеспечивается сочетанием минимальной внутригрупповой вариации и максимальной межгрупповой вариации.
7. По каждому i-му объекту (i = 1, 2, ..., N) множества М определяется соответствующее значение дискриминантной функции:
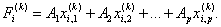
8. По совокупности найденных значений F(k) рассчитываются средние значения для каждого подмножества Mk:
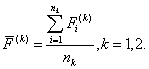
9. Определяется общее среднее (константа дискриминации) для дискриминантных функций
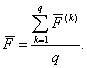
10. Выполняется распределение (дискриминация) объектов подмножества М0 подлежащих дискриминации по обучающим выборкам М1 и М2. С этой целью рассчитанные и п. 7 по каждому i-му объекту значения дискриминантных функций
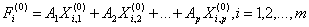
сравниваются с величиной 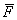 общего среднего. На основе сравнения данный объект относят к одному из обучающих
подмножеств.
общего среднего. На основе сравнения данный объект относят к одному из обучающих
подмножеств.
Если 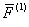 >
>
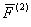 , то i-й объект подмножества
М0 относят к подмножеству М1, при
, то i-й объект подмножества
М0 относят к подмножеству М1, при
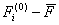 > 0 и к подмножеству М2
при
> 0 и к подмножеству М2
при 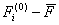 < 0. Если же
< 0. Если же
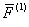 <
< 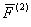 ,
то заданный объект относят к подмножеству М1, при
,
то заданный объект относят к подмножеству М1, при
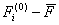 < 0 и к подмножеству М2
в противном случае.
< 0 и к подмножеству М2
в противном случае.
11. Далее делается оценка качества распределения новых объектов, для чего оценивается вклад переменных в дискриминантную функцию.
Влияние признаков на значение дискриминантной функции и результаты классификации может оцениваться по дискриминантным множителям (коэффициентам дискриминации), по дискриминантным нагрузкам признаков или по дискриминантной матрице.
Дискриминантные множители зависят от масштабов единиц измерения признаков, поэтому они не всегда удобны для оценки. Дискриминантные нагрузки более надежны в оценке признаков, они вычисляются как парные линейные коэффициенты корреляции между рассчитанными уровнями дискриминантной функции F и признаками, взятыми для ее построения.
Дискриминантная матрица характеризует меру соответствия результатов классификации фактическому распределению объектов по подмножествам и используется для оценки качества анализа. В этом случае дискриминантная функция F формируется по данным объектов (с измеренными p признаками) обучающих подмножеств, а затем проверяется качество этой функции путем сопоставления фактической классовой принадлежности объектов с той, что получена в результате формальной дискриминации.
Пример применения дискриминантного анализа при наличии двух обучающих выборок (q=2)2. Имеются данные по двум группам промышленных предприятий отрасли:
Х1 - среднегодовая стоимость основных производственных фондов, млн. д.ед.;
Х2 — среднесписочная численность персонала, тыс. чел.;
Х3 — балансовая прибыль млн. д.ед.
Исходные данные представляются в табличной форме
| Номер группы Mk (k = 1, 2) | Номер предприятия, i (i = 1, 2, ..., nk3) | Свойства (показатель), j (j = 1, 2, ..., p) | ||
|---|---|---|---|---|
| Х1 | Х2 | Х3 | ||
| Группа 1, M1 (k = 1) | 1 | 224,228 | 17,115 | 22,981 |
| 2 | 151,827 | 14,904 | 21,481 | |
| 3 | 147,313 | 13,627 | 28,669 | |
| 4 | 152,253 | 10,545 | 10,199 | |
| Группа 2, M2 (k = 2) | 1 | 46,757 | 4,428 | 11,124 |
| 2 | 29,033 | 5,51 | 6,091 | |
| 3 | 52,134 | 4,214 | 11,842 | |
| 4 | 37,05 | 5,527 | 11,873 | |
| 5 | 63,979 | 4,211 | 12,860 | |
| Группа предприятий M0, подлежащих дискриминации | 1 | 55,451 | 9,592 | 12,840 |
| 2 | 78,575 | 11,727 | 15,535 | |
| 3 | 98,353 | 17,572 | 20,458 | |
Необходимо провести классификацию (дискриминацию) трех новых предприятий, образующих группу М0 с известными значениями исходных переменных.
Решение.
1. Значения исходных переменных для обучающих подмножеств M1 и M2 (групп предприятий) записываются в виде матриц X(1) и X(2)
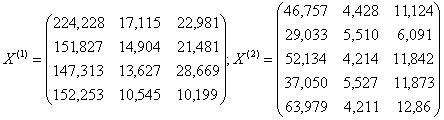
и для подмножества M0 группы предприятий, подлежащих классификации в виде матрицы X(0)

Общее количество предприятий, составляющих множество М, будет равно N = 3+4+5 = 12 ед.
2. Определяются элементы векторов
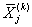 средних значений по j признакам
для i-х объектов по каждой k-й выборке (k = 1, 2),
которые представляются в виде двух векторов
средних значений по j признакам
для i-х объектов по каждой k-й выборке (k = 1, 2),
которые представляются в виде двух векторов
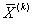 (по количеству обучающих выборок):
(по количеству обучающих выборок):
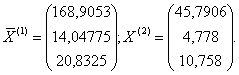
3. Для каждого обучающего подмножества M1 и M2 рассчитываются ковариационные матрицы Sk (размером р×р):
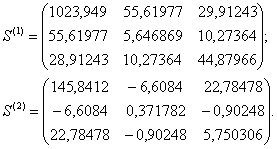
4. Рассчитывается объединенная ковариационная матрица:
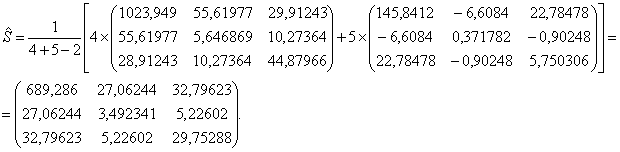
5. Рассчитывается матрица 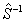 обратная к объединенной ковариационной матрице:
обратная к объединенной ковариационной матрице:

6. Рассчитываются дискриминантные множители (коэффициенты дискриминантной функции) по всем элементам обучающих подмножеств:
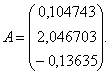
7. Для каждого i-го объекта k-го подмножества М определяется значение дискриминантной функции:

8. По совокупности найденных значений F(k)
рассчитываются средние значения 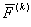 для каждого
подмножества Mk:
для каждого
подмножества Mk:
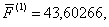
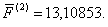
9. Определяется общее среднее (константа дискриминации) для дискриминантных функций:
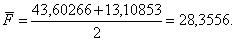
10. Выполняется распределение объектов подмножества М0 по обучающим подмножествам М1 и М2, для чего по каждому объекту (i = 1, 2, 3) рассчитываются Дискриминантные функции
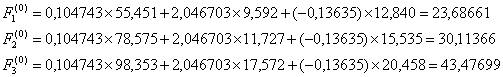
и затем рассчитанные значения дискриминантных функций F(0)
сравниваются с общей средней 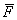 = 28,3556.
= 28,3556.
Поскольку 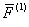 >
>
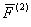 , то i-й объект подмножества
М0 относят к подмножеству М1 при
, то i-й объект подмножества
М0 относят к подмножеству М1 при
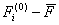 > 0 и к подмножеству М2
при
> 0 и к подмножеству М2
при 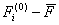 < 0. С учетом этого в данном примере
предприятия 2 и 3 подмножества М0 относятся к М1,
а предприятие 1 — к М2.
< 0. С учетом этого в данном примере
предприятия 2 и 3 подмножества М0 относятся к М1,
а предприятие 1 — к М2.
Если бы выполнялось условие
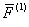 <
< 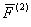 ,
то объекты М0 относились к подмножеству М1,
при
,
то объекты М0 относились к подмножеству М1,
при 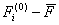 < 0 и к подмножеству М2
в противном случае.
< 0 и к подмножеству М2
в противном случае.
11. Оценку качества распределения новых объектов выполним путем
сравнения с константой дискриминации 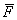 значений дискриминантных функций
значений дискриминантных функций 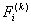 обучающих
подмножеств М1 и М2. Поскольку для всех
найденных значений выполняются неравенства
обучающих
подмножеств М1 и М2. Поскольку для всех
найденных значений выполняются неравенства
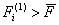 , и
, и 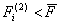 ,
то можно предположить о правильном распределении объектов и уже существующих
двух классах и верно выполненной классификации объектов подмножества
М0.
,
то можно предположить о правильном распределении объектов и уже существующих
двух классах и верно выполненной классификации объектов подмножества
М0.
Литература по теме 6
1. Айвазян С.А., Мхитарян B.C. Прикладная статистика и основы эконометрики. - М.: ЮНИТИ, 1998. — 1022 с.
2. Глинский В.В., Ионин В.Г. Статистический анализ. Учебное пособие. — М.: Информационно-издательский дом «Филинъ», 1998.- 264 с.
3. Дубров A.M., Мхитарян B.C., Трошин Л.И. Многомерные статистические методы: Учебник. - М.: Финансы и статистика, 1998. - 352 с.
4. Клаичев А.П. Методы и средства анализа данных в среде Windows. STADIA 6.0. — М.: Информатика и компьютеры, 1998. - 270 с.
5. Сошникова Л.А., Тамашевич В.Н. и др. Многомерный статистический анализ в экономике: Учебное Пособие для вузов / Под ред. проф. В.Н. Тамашевича.— М.: ЮНИТИ-ДАНА, 1999. - 558 с.
6. Факторный, дискриминантный и кластерный анализ: Пер. с англ. / Под ред. И.С. Енюкова. — М.: Финансы и статистика, 1989. — 215 с.
7. Компьютерные технологии экономико-математического моделирования: Учебное пособие. / Под ред. Д.М. Дайитбегова, И.В. Орловой. - М.: ЮНИТИ, 2001.
1 Здесь nk — объем обучающей выборки в k-м подмножестве.
2 Расчеты данного примера выполнялись в среде EXCEL.
3 Здесь nk — объем обучающей выборки в k-м подмножестве.